Автомобилизация и дорожное движение. Характеристика дорожного движения. Задержка движения. Исследование дорожного движения. Анализ дорожно-транспортных происшествий, страница 5

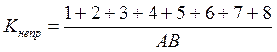
Коэффициент непрямолинейности:

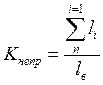
Важное значение для улично-дорожной сети имеет топологическое расположение (расположение как в плане так и в профиле).

Пешеходный поток.

Улично-дорожная сеть и эффективность её работы зависит от пешеходного потока. Так как пешеходный поток является своеобразным стимулом для выбора режимов движения транспортных средств. Он характеризуется скоростью, интенсивностью и плотностью (скорость пешехода – 0,5-1,5м/с).

Плотность пешеходного потока взаимосвязана с возникновением помех в движении пешеходного потока. Уже при плотности 0,5 чел/м² начинает возникать дискомфорт в движении пешеходов. Движение пешеходов характеризуется следующим образом:

по тротуару: свободное    0,6-0,8 м/с;

                       стесненное  0,4-0,5 м/с;

по наземным пешеходным переходам:

при малой плотности        1,1-1,3 м/с;

при высокой плотности    0,8-1 м/с

Скорость движения пешеходов является субъективным фактором

Движение пешеходов в колонне характеризуется динамической длиной. Она равна 2 м. с учетом дистанции между впереди движущимися пешеходами.

Математическое описание транспортного потока.

Математическое описание транспортного потока осуществляется с целью выработки модели, которая хотя бы равноценно соответствовала реально складывающимся условиям на конкретном участке автодороги.

Наиболее распространенные математические модели:

-  детерминированные – модели, в которых обособленно рассматривается какой-то фрагмент потока на заданном участке дороги и вся протяженность пути складывается из таких фрагментов.

В этом моделировании используют формальные выражения , для которых характерно применение  конкретных цифр и значений, поэтому формулы записываются в виде зависимостей и отношений одной величины к другой.

-  стохастические – это модели, базирующиеся на обработке случайно наблюдаемых величин, установлении закономерностей их изменения, которые выбираются в последующем из теоретически известного массива законов и применяются для полного описания транспортного потока.

В этих моделях в основу положено допущение о том, что все происходящие в потоке события носят случайный вероятностный характер. Эти модели являются базой для разработки программ, используемых в динамическом моделировании решаемых задач на компьютере.

Структурно это выглядит следующим образом: на основании наблюдений определяется закон распределения случайных величин, после чего устанавливается связь между случайными величинами, разрабатывается блок-схема и алгоритм модели, для которых пишется программа, затем посредством введения в компьютер данных о состоянии потока производится расчет требуемых значений из числа которых выбирается оптимальное значение. Результатом обследования является получение формальных зависимостей и связей. с помощью которых устанавливается закономерность изменений свойственных транспортному потоку. В частности, строится диаграмма транспортного потока, зависимость плотности потока от скорости движения транспортного средства. Используя её, имеется возможность определить экстремальное значение плотности.

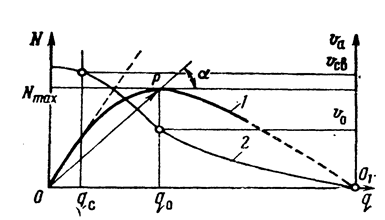
Рис.5 Диаграмма транспортного потока.

 ;                             

- скорость свободного движения

-плотность потока, соответствующая максимально возможной интенсивности;

-угол наклона радиуса – вектора, характеризующий скорость транспортного потока.

Эта диаграмма дает возможность обозначить распределение плотности транспортного потока, зависит от характера кривой. Первая кривая является параболической, вторая кривая линейно изменяется и отображает экстремальное значение в точке перегиба, она также описывается определенной зависимостью, которая может быть положена в основу описания транспортного потока.

Интенсивность и пропускная способность.