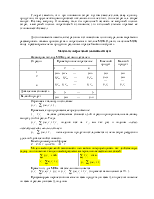
Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат

Целевые установки развития и типы экономических моделей

Вводные понятия обозначения, формулировка задачи

Рассмотрим экономику, как объединение двух сфер:

Сфера производства, включающая различные виды деятельности jN₁. В число видов деятельности включаются процессы производства продукции и услуг и доведение производимой продукции до конечного потребителя.

Сфера потребления, включающая использование конечных благ iN₂ для удовлетворения потребностей общества.

Соответственно общий вектор переменных модели делится на две части, интенсивность видов деятельности характеризуется вектором X₁ = (x_j) – иначе вектор объёмов производства по каждому виду деятельности, а объемы использования благ – вектором X₂ = (x_i) . Общий вектор:

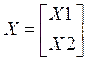                                     ,         N₁N₂ = N

 Балансы модели разделяются также на две группы:

·  балансы производства и использования различных видов продукции

·  ограничения по ресурсам

Общий индекс продукции – s₁M₁, причём N₂M₁. Так как не все виды продукции потребляются конечными потребителями. Например, руда это один из видов продукцииM₁,однако руда используется исключительно для промежуточного потребления N₂.  Множество M₁ шире.

Общий индекс ресурсов – s₂M₂. При этом  М₁ М₂ =М.

Далее…

g₁(X₁) = {g_s1(X₁)}, где s₁M₁ – вектор-функция выпуска продукции сферы производства (т.е. разность между произведенной и использованной продукцией в сфере производства);

g₂(X₁) = {g_s2(X₁)}, где s₂M₂   – вектор-функция затрат ресурсов.

Q = (q_s1) – вектор фиксированных объёмов использования продукции в сфере потребления (использование продукции государством, затраты на оборону и тому подобное).

R = (r_s2) – вектор объёмов имеющихся ресурсов.

F(X) = [f^k(X), U(X₂)] – векторная целевая функция благосостояния. Является композицией функции полезности потребителей U(X₂) и набора других целевых функций f^k(X), выражающих другие однородные, непосредственно несводимые цели общества, такие как повышения материального благосостояния, обеспечение безопасности государства, развитие системы качественного образования или здравоохранения и т.д.

Итак, нашей основной задачей является нахождения  вектора X, который доставляет максимум целевой функции и при этом удовлетворяет неким ограничениям, формирующим допустимое множество. Формализуем эту задачу.

Одноуровневая модель с глобальным критерием оптимальности

F(X) → max

g₁(X₁)  X₂ + Q                        экономика должна удовлетворить весь спрос

g₂(X₁)  R                                 затраты не могут превышать имеющиеся ресурсы

X₁, X₂   0                                 ограничение на неотрицательность переменных

g₁(X₁)  0                                  условие продуктивности экономической системы

Если последнее условие не выполнено это означает, что мы попросту портим ресурсы, затрачиваем больше чем производим.

Модель называется одноуровневой, так как максимизируется единая целевая функция в один этап. В отличие от многоуровневой задачи, где единая задача нахождения оптимального решения распадается на ряд взаимосвязанных оптимизационных задач меньшей размерности, затем решение общей задачи представляет собой итерационный процесс согласования решений отдельных задач.

Фраза «С глобальным критерием оптимальности», означает, что модель нацелена на поиск глобального максимума на допустимом множестве.

Решать задачу векторной оптимизации в таком виде довольно трудно. Поэтому векторную целевую функцию обычно сводят к скалярной. Для решения той задачи имеется хорошо разработанный математический аппарат.

Скаляризация

а) Одним из приёмов формирование следующей функции (в ТИГРОРе она называлась α-ФСБ, сейчас её наверное следовало бы назвать λ-ФСБ)

F(X) = λ₀U(X₂) +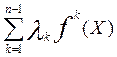

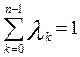
Опять же из ТИГРОРа, можно вспомнить теоремку, что любое решение данной задачи даёт X* - слабый  оптимум по Парето, и если  для любого k, то X* - сильный оптимум по Парето. Такие сильные оптимумы по Парето называются в данном курсе эффективными вариантами (решениями), либо оптимальными решениями.

Таким образом, решая данную задачу для различных λ, мы получаем некоторое множество эффективных решений. Следовательно, область выбора сужается от множества допустимых вариантов к множеству эффективных вариантов. Следующий этап выбора решения представляет собой выбор компромисса.

В случае если λ – орт (имеет одну ненулевую компоненту равную единице), получаем решения, которые называются субоптимальными.

Данный вид скаляризации хорош также тем, что выбор λ задаёт расстановку приоритетов в обществе (каждая целевая функция входит с определенным весом, в зависимости, от её значимости).

б)    Можно также скаляризовать функцию F(X) следующим образом. Этот метод называется – Методом справедливого компромисса.

F(X) =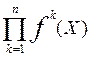

В этой функции заложен принцип: справедливым считается такой компромисс, когда при сравнении вариантов решений относительное снижение по одним критериям не превосходит относительного повышения по другим. Кроме того, в таком представлении ни одна функция не может занулиться.