Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 6

4.   – Леонтьевская функция, характеризует взаимодополняемые товары. Увеличение потребления одного или нескольких благ, без увеличения потребления дополняемых благ не приводит к росту целевой функции.

5.   – квазилинейная функция, одно благо входит линейно, все остальные нет.

Соизмеримость и взаимозаменяемость потребительских благ

Разнообразные по своему назначению потребительские блага непосредственно несравнимы между собой, довольно трудно сравнивать палку колбасы и билет в театр. Однако самые разнообразные потребительские блага сравнимы в том смысле, что их потребление увеличивает значение функции благосостояния. То есть показатели общественной полезности благ выводятся из целевой функции. Частные производные 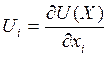 характеризуют прирост общего уровня благосостояния в результате увеличения потребления i-го блага на малую единицу, то есть предельную полезность i-ого блага.

Стоит заметить, что неоднозначность (с точность до монотонно возрастающего преобразования) определения целевой функции имеет своим следствием неоднозначность частных производных, однако отношение частных производных остаётся неизменным.

Общее изменение значения  целевой функции можно представить в виде

.

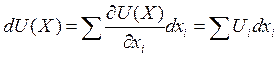Из этой формулы следует, что прирост функции социального благосостояния может, достигнут разными путями. В этом – основа взаимозаменяемости  благ. Отсюда же мы можем выразить коэффициент замены одного блага другим. Посмотрим, насколько, при изменении потребления одного блага, надо изменить потребления одного блага, чтобы оставить уровень полезности на том же уровне. Если уровень благосостояния не изменяется, то . Из этой формулы выводятся эквивалентные нормы взаимозаменяемости благ. Допустим количества всех благ, кроме k и j не изменяются, тогда имеем , откуда

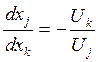 таким образом, норма эквивалентной замены j-го блага k-ым обратно пропорциональна соотношению полезностей этих благ, взятому с обратным знаком.

Анализ модели поведения потребителя

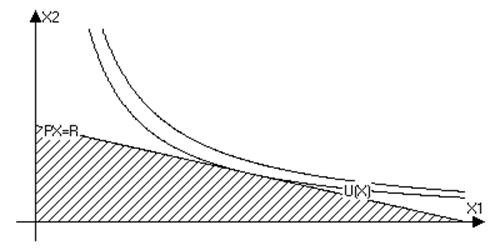Пусть имеется n товаров. Спрос потребителей на эти товары задан вектором , цены  вектором , а величина дохода R. Тогда простейшую модель поведения потребителя можно представить в виде:

                     

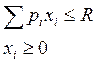    или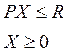         

Выясним условия оптимальности данной модели:

Функция Лагранжа: , тогда условия Куна-Таккера записываются следующим образом:

 для всех i=1, …, n

 при

Если же , то данный товар не приобретается. Кроме того,  соответствует полному использованию дохода: .

Тогда можем записать:

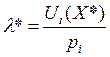 если  далее

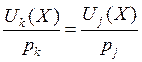, если  или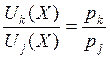 

Это означает, что потребители должны выбирать товары таким образом, чтобы отношение придельной полезности к цене товара было одинаково для всех товаров или, что равносильно, предельные полезности выбираемых товаров должны быть пропорциональны ценам.

Рассмотрим два примера нахождения спроса на блага.

Пример 1.

Получаем  и  

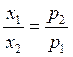
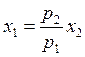
 подставляем в , имеем

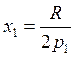и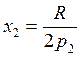

Пример 2.

Рассмотрим модель, где есть два блага потребление (x) и свободное время (h)

Доход индивида потребителя складывается из его трудового дохода (– ставка заработной платы на количество отработанного времени) и прочих доходов (R). Тогда бюджетное ограничение переписывается следующим образом:

Но количество свободного и рабочего времени фиксировано, т.е. , тогда

Итак, имеем следующую задачу:

Решая эту задачу аналогичным образом, получим:

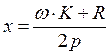 и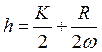

В принципе, это ответ, но из этой задачи можно получить еще кое-что. Так как ,  то из последнего выражения, получим:

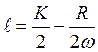 – это не что иное, как функция предложения труда.

Дифференциальные соотношения и эластичность спроса от дохода и от цены

По знаку частных производных спроса на i-ое благо, мы можем определить тип данного блага, а также  взаимозаменяемость и дополняемость различных благ.

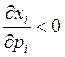 – нормальное благо, с ростом цены спрос на это благо уменьшается.

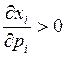– товары Гиффена (например, картофель) или спрос на товары во время инфляции, с ростом цены спрос на эти товары возрастает.

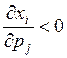 – взаимодополняемые товары, рост цены на j-ый товар приводит к уменьшению спроса на i-ый товар.