· и саму единицу конечной продукции (если i=j), которую нужно произвести; за это отвечает единичная матрица E.
Следует заметить, что при понимании затрат в узком смысле слова, саму единицу продукции, которую необходимо произвести включать в них не стоит, это не затраты, а скорее выпуск. Поэтому матрицу B по-моему было бы правильней называть не матрицей полных затрат, а матрицей полных потребностей в экономике, это в большей степени отражает её экономический смысл.
До этого момента нам было без разницы в стоимостном или в натуральном выражении рассматривать объёмы производства и потребления в таблице МОБ. Однако, на основе МОБ, вводя в рассмотрение цены продукции различных отраслей можно построить
Модель межотраслевой зависимости цен
Рассмотрим таблицу МОБ с учетом индекса цен.
|
Отрасли |
Промежуточное потребление |
Конечный продукт |
Валовой продукт |
|
1 2 ... n |
|||
|
1 2 n |
…
|
…
|
…
|
|
Добавленная стоимость |
|
||
|
Валовой продукт |
|
||
Обратимся к балансу по столбцам:
![]()
Примем ещё одно упрощающее предположение:
![]() – валовая добавленная стоимость j-ой отрасли пропорциональна валовому выпуску этой отрасли.
Тогда
– валовая добавленная стоимость j-ой отрасли пропорциональна валовому выпуску этой отрасли.
Тогда
![]() поделив всё на
поделив всё на ![]() , мы как
раз и получим модель межотраслевой зависимости цен.
, мы как
раз и получим модель межотраслевой зависимости цен.
![]() – цена единицы продукции складывается
из цены затрат ресурсов и удельной добавленной стоимости.
– цена единицы продукции складывается
из цены затрат ресурсов и удельной добавленной стоимости.
В векторно-матричной форме
![]() или
или ![]()
Модель межотраслевой зависимости цен можно интерпретировать как двойственную задачу по отношению к модели межотраслевых материально-вещественных связей:
|
|
|
Кроме того, для МОБа обязательно выполняется
![]() и
и ![]() эти
равенства выполняются
эти
равенства выполняются ![]() .
.
Просуммируем первое соотношение по всем продукта (по всем i), второе соотношение по всем отраслям (по всем j), получим
![]() и
и ![]()
Теперь посмотрим, что мы получили:
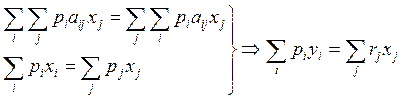
то есть объём созданной в экономике конечной продукции (в стоимостном выражении) равен суммарной валовой добавленной стоимости. Данное соотношение эквивалентно условию равенства функционалов прямой и двойственной задачи.
Теперь попробуем посмотреть на r с другой стороны, обратим внимание на те компоненты, из которых складывается добавленная стоимость.
![]() , где
, где
![]() – общий фонд заработной платы в отрасли;
– общий фонд заработной платы в отрасли;
![]() – прибыль;
– прибыль;
![]() –амортизация в j-ой
отрасли.
–амортизация в j-ой
отрасли.
Переходя к удельным показателям, имеем:
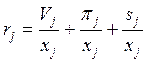
Теперь мы можем переписать модель межотраслевых зависимостей цен следующим образом:
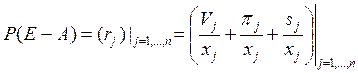 или
или 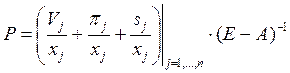
Модель, записанная в таком виде, позволяет нам прогнозировать уровень цен на различные виды продукции при изменении ставок заработной платы, норм прибыльности и норм амортизации в различных отраслях.
Если ввести ряд дополнительных предположений, то модель можно ещё немного видоизменить.
Итак, среднюю ставку заработной платы по отрасли, можно определить как частное фонда заработной платы на количество занятых в данной отрасли, т.е.
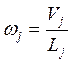 .
.
Удельную
амортизацию, в свою очередь, можно представить как ![]() , где
, где ![]() – единая
норма выбытия основного капитала, а
– единая
норма выбытия основного капитала, а ![]() , соответственно,
уровень этого капитала.
, соответственно,
уровень этого капитала.
Прибыль можно
так же представить в виде: ![]() , где i – доходность на капитал.
, где i – доходность на капитал.
Кроме того
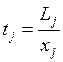 – трудоёмкость j-ой
отрасли;
– трудоёмкость j-ой
отрасли;
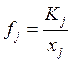 – фондоёмкость j-ой
отрасли
– фондоёмкость j-ой
отрасли
С учетом введенных соотношений удельную добавленную стоимость можно переписать следующим образом:
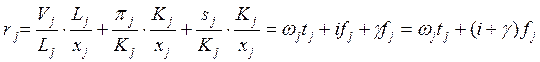
Здесь ![]() можно интерпретировать как валовую ставку
кредита. И модель межотраслевой зависимости цен перепишется соответственно
можно интерпретировать как валовую ставку
кредита. И модель межотраслевой зависимости цен перепишется соответственно
![]()
Теперь мы можем прогнозировать возможный уровень цен в зависимости от изменения ставки заработной платы, валовой ставки процента, трудоемкости и фондоемкости.
Введем в модель ограничения на ресурсы. Теперь модель межотраслевого баланса должна удовлетворять следующим соотношениям:
![]() , где k= 1,…, K – индекс ресурса (первичного
фактора). Данное соотношение можно переписать в матричной форме:
, где k= 1,…, K – индекс ресурса (первичного
фактора). Данное соотношение можно переписать в матричной форме:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.