Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 18

Видим, что эти предположения слишком жесткие и едва ли выполнены в реальной жизни, поэтому подробно останавливаться на рассмотрении этого вида дискриминации мы не будем.

Ценовая дискриминация второго типа

Здесь предполагается, что монополист не имеет возможности предлагать разным потребителям разные сделки, допустим потому что он не умеет их различать, то есть не знает ту цену на которую согласится каждый конкретный потребитель  Цена на благо зависит от количества приобретаемого блага. В качестве примера можно привести скидки для оптовых покупателей или зависимость тарифа на телефонные переговоры от продолжительности. То есть при дискриминации второго типа с разных потребителей монополист берет одинаковую плату за одно и тоже количество товара.

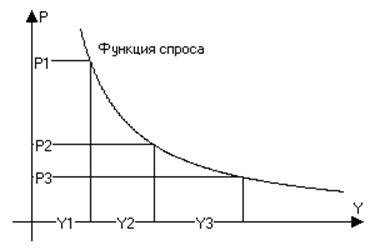Пусть монополист предлагает n партий (пакетов) товаров различных объёмов, по различным ценам. Его задача состоит в том, чтобы выбрать объёмы партий таким образом, чтобы получить наибольшую прибыль. Если покупатель приобретает товар в объёме меньшем чем , то его цена определяется из обратной функции спроса следующим образом . Причем это цена самая высокая. Если покупатель покупает больше чем , то на величину , он получает скидку, т.е. на этот объём цена равна . Далее если покупатель покупает больше чем , то цена партии  равна . И так далее…

Введём следующие обозначения:

…

 Тогда общая прибыль производителя запишется следующим образом:

Будем рассматривать случай , перепишем функцию прибыли:

На всякий случай распишем взятие дифференциала от функции затрат:

Условия равновесия:

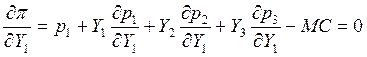
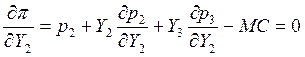
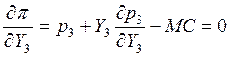
Вспомним что такое придельный доход :

Общий доход или общая выручка от реализации i-го продукта:

Придельный доход: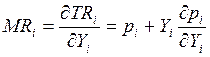

Таким образом, третье условие равновесия можно переписать следующим образом:

 

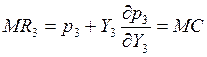
Выраженные таким образом придельные издержки подставляем во второе условие:

      (**)

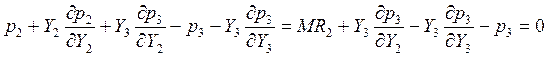Покажем что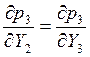

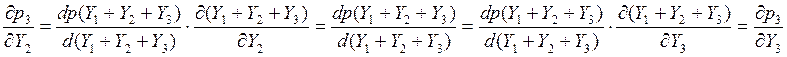
Ну да жутковато, но это только на первый взгляд ;)

Теперь пользуясь полученным результатом в (**) получим:

Теперь из  второго условия выразим придельные издержки:

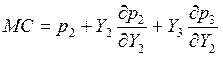, подставляем в первое:

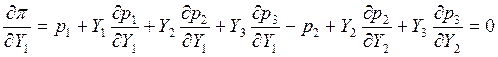
Пользуясь тем что

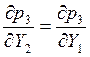 и 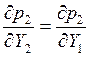 это выражение можно преобразовать к виду:

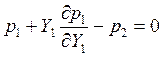
То есть:

В итоге мы получили следующие оптимальные условия

Данный результат можно обобщить и на случай, когда производитель выделяет n партий:

…

Ценовая дискриминация третей степени

Этот вид ценовой дискриминации связан с делением потребителей на группы (сегментирование рынка), в зависимости от эластичности спроса по цене. В качестве примера можно привести скидки студентам и пенсионерам. Дискриминация третьего типа осуществляется монополистом относительно типов потребителей вне зависимости от количества приобретаемых благ.

Функция прибыли монополиста имеет в таком случае следующий вид:

Для случая n=2:

 

Условия равновесия:

 

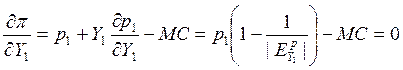
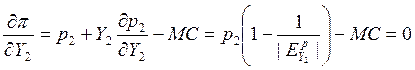
Оптимальное соотношение цен тогда определяется следующим образом:

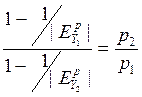
Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат

Производственные функции с взаимозаменяемыми ресурсами и функции производственных затрат отражают противоположные принципы сочетания ресурсов в производственных процессах (взаимозаменяемость и взаимодополняемость). Поэтому может показаться, что между этими моделями нет никакой связи, однако, покажем, что это не так.

Введем понятие изоклинали.

Изоклиналь – кривая в пространстве ресурсов с одинаковыми нормами эквивалентной замены.

Поэтому взаимозаменяемость ресурсов  в производстве можно представить как переход от одной изоклинали к другой.

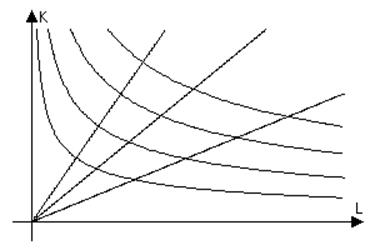
Рассмотрим на примере функции Кобба-Дугласа.

  

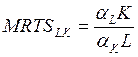
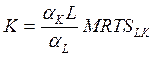
Таким образом, геометрически изоклиналь функции Кобба-Дугласа – это луч, исходящий из начала координат. В каждой точке этого луча соотношение используемых ресурсов одинаково. Разным соотношениям используемых ресурсов при меняющихся объёмах соответствуют разные лучи.

Зафиксируем значение нормы технологического замещения: . И обозначим , ,   –  объёмы производства и затрат, соответствующие изоклинали . Тогда можем записать следующее: