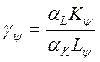
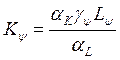 и
и 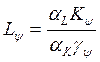
Подставляем первое выражение в производственную функцию
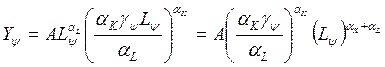 (*)
(*)
Аналогично для капитала:
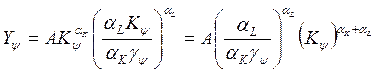 (**)
(**)
При сбалансированности ресурсов эти два равенства должны выполняться одновременно.
Пусть
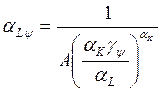 и
и 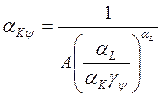 ,
кроме того
,
кроме того ![]()
Тогда выражения (*) и (**) можно объединить в функцию с взаимодополняемыми ресурсами:
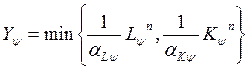 .
.
То есть мы перешли от функции с взаимозаменяемыми ресурсами к функции с взаимодополняемыми ресурсами, соответствующей ψ-му соотношению ресурсов.
Отсюда можно перейти к функциям производственных затрат.
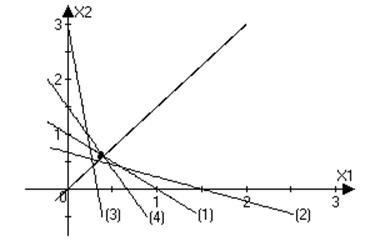
Продемонстрируем полученный результат на рисунке:
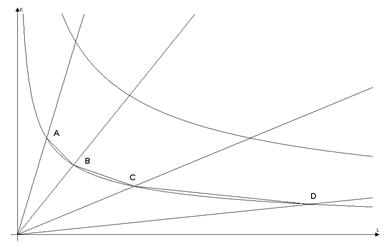 На
графике точки A, B, C, и D характеризуют количества
затрачиваемых ресурсов для получения одного и того же объёма выпуска. Соединив
эти точки мы получаем ломаную, которая аппроксимирует изокванту
производственной функции Кобба-Дугласа. Чем больше проведено изоклиналей, тем
лучше ломаная аппроксимирует изокванту.
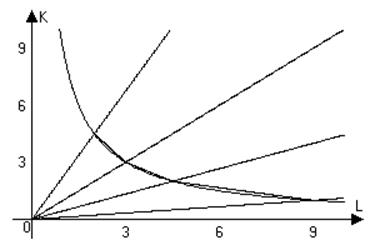
На
графике точки A, B, C, и D характеризуют количества
затрачиваемых ресурсов для получения одного и того же объёма выпуска. Соединив
эти точки мы получаем ломаную, которая аппроксимирует изокванту
производственной функции Кобба-Дугласа. Чем больше проведено изоклиналей, тем
лучше ломаная аппроксимирует изокванту.
То есть если мы имеем семейство изоклиналей, то, зафиксировав объём производства и меняя один из ресурсов, мы можем восстановить изокванты производственной функции. Вот такая взаимосвязь!
Для лучшего понимания этой запутанной темы рассмотрим задачку, к тому же подобные задачки порой бывают на экзамене.
Пример:
Даны точки изокванты производственной функции Кобба-Дугласа (то есть, даны определенные производственные способы):
![]()
|
(L, K) |
(3, 3) |
(2, 4.5) |
(9, 1) |
(4.5, 2) |
Всего в экономике имеются следующие запасы ресурсов: L=15; K=10.
Определить: 1. Какие изоклинали задаются этими точками;
2. оптимальную интенсивность использования производственных способов.
Решение:
Итак, изоклинали, это кривые с одинаковыми нормами эквивалентной замены, то есть изоклинали как раз и задаются нормой замены (MRTS), поэтому посчитаем норму замены для каждой из представленных точек.
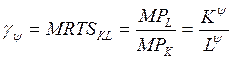
рассчитываем
![]()
![]()
![]()
![]()
Изоклинали определили.
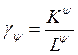
![]()
![]() ,
, 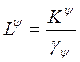
![]()
![]()
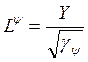
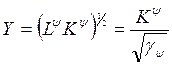
![]()
![]()
Теперь можем записать производственную функцию, как функцию с взаимодополняемыми ресурсами:
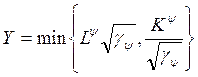
Далее, выразим для каждого производственного способа необходимое количество труда и капитала, через интенсивность использования этого производственного способа:
|
|
|
|
|
Составляем следующую задачу:
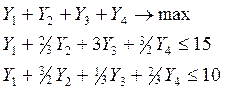
Двойственная задача:
![]()
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Решая
двойственную задачу, получаем оптимальное решение на пересечении (1) и (4)
ограничений. А все остальные ограничения выполняются как строгие неравенства,
значит, соответствующие им переменные исходной задачи, равны нулю (условие
дополняющей нежесткости). То есть ![]() . Тогда
. Тогда
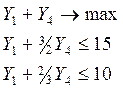
![]()
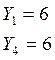
Итак, получили, что в оптимальный план будут входить только первый и четвёртый способы, интенсивность использования каждого их них будет равна шести.
Задача общего равновесия Эрроу-Дебре
Модель совершенного рынка Эрроу-Дебре называется также классической или неоклассической, так как она ведет своё начало от идей Адама Смита и Дэвида Риккардо. Главная идея состоит в объяснении возникающих в рыночной экономике пропорций производства, потребления и цен. Модель базируется на следующих предположениях:
1. потребители и производители действуют в условиях одинаковых цен;
2. все рынки конкурентные;
3. продаваемая продукция однородна;
4. количество покупателей и продавцов большое, они анонимны и владеют всей информацией, следовательно, могут мгновенно принимать решения;
5. нет барьеров на вход и на выход в любой отрасли, то есть начать и прекратить производство любого из продуктов можно мгновенно.
Вспомним и уточним некоторые обозначения и индексы:
Пусть в экономике имеется K потребителей и l фирм.
Общий вектор
переменных модели делится на две части: интенсивность видов деятельности
характеризуется вектором ![]()
![]() ,
а объемы использования благ – вектором
,
а объемы использования благ – вектором ![]()
![]() . Общий вектор:
. Общий вектор:
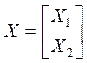 ,
, ![]()
Общий индекс
продукции – s1![]() M1, причём N2
M1, причём N2![]() M1. Так
как не все виды продукции потребляются конечными потребителями, существует
также промежуточное потребление.
M1. Так
как не все виды продукции потребляются конечными потребителями, существует
также промежуточное потребление.
Общий индекс
первичных ресурсов – s2![]() M2.
M2.
![]() , где s1
, где s1![]() M1 –
вектор-функция выпуска продукции сферой производства;
M1 –
вектор-функция выпуска продукции сферой производства;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.