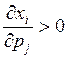 – взаимозаменяемые товары, рост цены на j-ый товар приводит к тому, что потребитель начинает покупать
большее количество i-ого товара.
– взаимозаменяемые товары, рост цены на j-ый товар приводит к тому, что потребитель начинает покупать
большее количество i-ого товара.
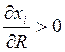 – нормальные товары, с ростом дохода
потребителя, он увеличивает спрос на данный товар.
– нормальные товары, с ростом дохода
потребителя, он увеличивает спрос на данный товар.
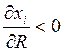 – малоценные товары, когда индивид
становится богаче, он сокращает их потребление (дешёвая одежда).
– малоценные товары, когда индивид
становится богаче, он сокращает их потребление (дешёвая одежда).
Для характеристики относительного изменения спроса используют коэффициенты эластичности.
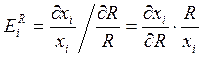 – коэффициент эластичности спроса на товар
i от дохода, характеризует
относительное изменение спроса по отношению к относительному изменению дохода.
На сколько изменится спрос на данное благо при изменении дохода на единицу.
– коэффициент эластичности спроса на товар
i от дохода, характеризует
относительное изменение спроса по отношению к относительному изменению дохода.
На сколько изменится спрос на данное благо при изменении дохода на единицу.
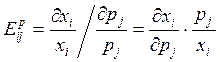 – коэффициент эластичности спроса на товар
i от цены товара j, характеризующий относительное изменение спроса при
относительном изменении цены.
– коэффициент эластичности спроса на товар
i от цены товара j, характеризующий относительное изменение спроса при
относительном изменении цены.
Эластичность спроса по цене
В зависимости от значения коэффициента эластичности все товары делятся на три группы:
·
Товары с неэластичным спросом ![]() ;
;
·
Торы с единичной эластичностью ![]() ;
;
·
Товары с высокоэластичным спросом ![]()
Эластичность спроса от дохода
Л. Торнквист разделил все товары на три группы, в зависимости от эластичности спроса на эти товары от дохода. Мы последуем его примеру.
1. Товары первой необходимости. Функция спроса на эти товары имеет вид
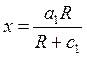 , где
, где ![]()
![]()
Она отражает тот факт, что рост
спроса на товары, удовлетворяющие насущные потребности, постепенно замедляется
(так, что 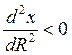 ). И имеет придел
). И имеет придел ![]() ,
при
,
при ![]() (т.е. кривая асимптотически приближается к
линии
(т.е. кривая асимптотически приближается к
линии![]() ).
).
2. Предметы второй необходимости или товары, эластичность которых близка к единице. Функция спроса:
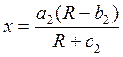 , при
, при ![]() и
и ![]() ,
, ![]() ,
, ![]() .
.
Эта функция так же имеет придел ![]() , но более высокого уровня чем
, но более высокого уровня чем ![]() . Спрос на эту группу товаров появляется,
только если уровень дохода превысил уровень
. Спрос на эту группу товаров появляется,
только если уровень дохода превысил уровень ![]()
3. Предметы роскоши, спрос на эту группу товары выражается следующей формулой.
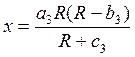 , при
, при
![]() и
и ![]() ,
, ![]() ,
, ![]()
Придел этой функции равен
бесконечности, спрос возникает только после того, как доход превысит ![]()
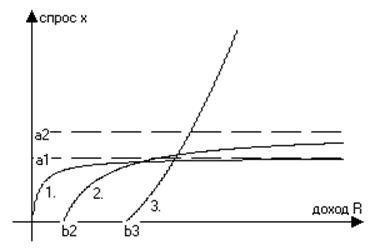 Однако
стоит понимать, что функции Торнквиста не всегда объективно отражают ситуацию,
они описывают только монотонное изменение спроса, в то время как функция спроса
может иметь S-образную форму, может иметь точки
максимума и точки перегиба.
Однако
стоит понимать, что функции Торнквиста не всегда объективно отражают ситуацию,
они описывают только монотонное изменение спроса, в то время как функция спроса
может иметь S-образную форму, может иметь точки
максимума и точки перегиба.
Выведем различные соотношения между эластичностями:
1. Для однородных функций есть такая формула Эйлера:
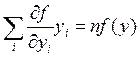 , где n это степень однородности.
, где n это степень однородности.
В качестве
функции![]() возьмём функцию спроса
возьмём функцию спроса ![]() , степень однородности этой функции ноль,
поэтому уравнение Эйлера переписывается следующим образом:
, степень однородности этой функции ноль,
поэтому уравнение Эйлера переписывается следующим образом:
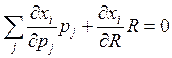
Делим обе
части на ![]() , получаем
, получаем
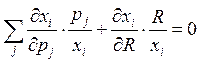 , или
, или 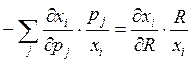
Видим, что левая часть этого равенства сумма эластичностей спроса на i-ый товар от j-ой цены, а правая часть эластичность спроса на i-ый товар от дохода. То есть данное равенство можно переписать следующим образом.
![]() – Вот такое хорошее равенство!
– Вот такое хорошее равенство!
2. Уравнение Энгеля (условие агрегации Энгеля)
Продифференцируем
по R бюджетное ограничение ![]() , получим
, получим
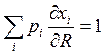
![]() – в принципе уже вот
эту штуку называют уравнением Энгеля. Однако её ещё можно по-преобразовывать.
Из следующих рассуждений.
– в принципе уже вот
эту штуку называют уравнением Энгеля. Однако её ещё можно по-преобразовывать.
Из следующих рассуждений.
На приобретение
каждого потребитель товара тратит определённую долю своего дохода, обозначим
эту долю – ![]() , то есть
, то есть
![]() , отсюда выражаем
, отсюда выражаем 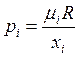 ,
подставляем это в уравнение
,
подставляем это в уравнение ![]() , получаем
, получаем
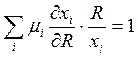 , узнаём эластичность спроса по доходу,
, узнаём эластичность спроса по доходу, ![]() – получаем, что средневзвешенная
эластичностей по доходу по всем товарам равна единице.
– получаем, что средневзвешенная
эластичностей по доходу по всем товарам равна единице.
3. Условие агрегации Курно
Теперь
продифференцируем бюджетное ограничение ![]() по
по ![]() ,
получим
,
получим
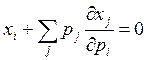 или
или 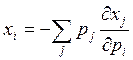
То есть спрос на i-ый товар равен отрицательной взвешенной изменений спроса на все товары от изменения цены i-го товара. Хотя это равенство также можно еще по-преобразовывать.
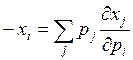
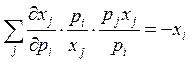 домножаем на
домножаем на ![]() и делим
на
и делим
на ![]() , получаем
, получаем
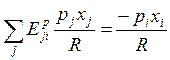
![]() . Если мы пробежимся по всем i, то получим следующее соотношение:
. Если мы пробежимся по всем i, то получим следующее соотношение:
![]() , где
, где ![]() -
вектор, составленный из
-
вектор, составленный из ![]() ; а
; а ![]() - матрица ценовых эластичностей.
- матрица ценовых эластичностей.
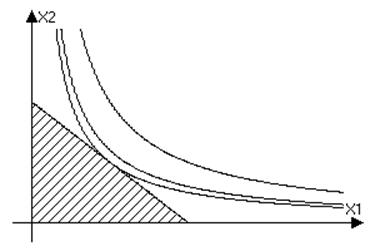
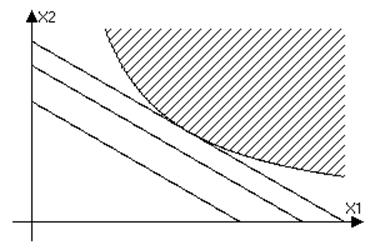
Косвенная функция полезности и ряд теорем с ней связанных
Задача A: Задача B:
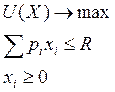
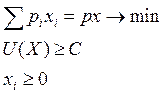
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.