Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 24

Эквивалентное определение продуктивности можно дать, опираясь на модель межотраслевых зависимостей цен.

Матрица A продуктивна, если можно подобрать такой неотрицательный вектор цен , который обеспечивает положительную валовую добавленную стоимость на единицу продукции, т.е. .

Условия продуктивности экономической системы:

Достаточное условие продуктивности:

Если матрица A неотрицательна и неразложима, то она продуктивна, если сумма элементов в каждом столбце строго меньше единицы –  .

Это условие достаточное, но не необходимое. Если оно выполнено, то мы заканчиваем анализ и говорим, что система продуктивна. Однако может случиться так, что система продуктивна, а это условие не выполняется. Но для любой продуктивной матрицы A можно подобрать такую новую систему цен, такую, что данное условие выполнится.

Необходимые и достаточные условия продуктивности:

1.  Все главные миноры матрицы (E-A) положительны.

2.  Все собственные числа матрицы A по модулю меньше единицы.

3.  Существует невырожденная матрица , все элементы которой неотрицательны.

Вообще если система продуктивна, то выполняются все эти три условия разом, т.е. нам для проверки продуктивности нам необходимо использовать одно из них. Если оно выполнится, то выполнятся и все остальные. Проверяем то условие, которое легче проверить.

Пример:

Даны три матрицы прямых затрат:

                                 

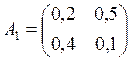
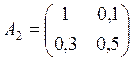
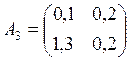
Определить: какие из приведенных матриц продуктивны, какие непродуктивны и какие продуктивны, но не удовлетворяют достаточному условию продуктивности.

Решение:

Начнём с матрицы , она продуктивна по достаточному условию. Посчитаем сумму по столбцам:

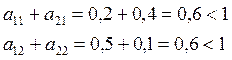
Матрица :

Сначала проверяем достаточное условие, видим, что оно не выполняется, но в данном случае это нам ничего не говорит о продуктивности данной матрицы.

Проверяем первое необходимое и достаточное условие:

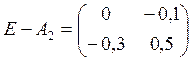, видим что первый главный минор , а для продуктивности необходимо, чтобы он был положительным. То есть матрица  непродуктивна.

Матрица :

Опять же видим, что по достаточному признаку эта матрица не проходит, сумма элементов по первому столбцу больше единицы. Проверяем необходимый и достаточный признак, для разнообразия, третий:

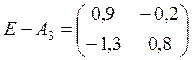 теперь посчитаем  матрицу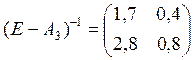

Видим, что эта матрица существует, и все её элементы неотрицательные, значит матрица   –  продуктивна.

Матрица полных затрат, матрица B

 Итак, вспомним основное тождество МОБа:

                      

Где B – это матрица полных затрат, она отражает соотношение между отраслевой структурой конечного продукта и отраслевой структурой валового выпуска. Коэффициент  определяет потребность в валовом общественном продукте для получения единицы конечной продукции отрасли j.

Например, если мы имеем следующую матрицу полных затрат

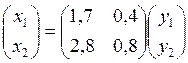
то  при росте конечного спроса на первую продукцию, в стоимостном выражении, на один рубль, первая отрасль должна увеличить валовой выпуск на 1,7 рублей, а вторая на 2,8 рублей, то есть в сумме на 3,5 рубля.

Матрицу  можно разложить следующим образом

Здесь следует провести аналогию с суммой бесконечно убывающей геометрической прогрессии.

Кроме того, повинуясь власти аналогий можно пойти ещё дальше, и вспомнить из  макроэкономики уравнение линии IS:

 

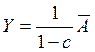
Выпуск равен произведению мультипликатора Кейнса на автономные расходы, в которые включается потребление, не зависящее от дохода, инвестиции гос. затраты  ит.д. Если мы посмотри на наше выражение

То можем найти ряд сходств. В нашем случае валовой выпуск определяется как произведение некоего матричного мультипликатора на конечный спрос. Исходя из этого, матрицу B часто называют матричным мультипликатором.

Кроме того, разложение  помогает нам содержательно понять смысл коэффициентов . Эти коэффициенты показывают, каковы полные потребности в выпуске продукции i, необходимые для получения единицы конечной  продукции вида j.  Они включают:

·  полные производственные затраты , которые в совою очередь состоят из прямых затрат (матрица A) и косвенных затрат (где матрица – косвенные затраты первого цикла,  – косвенные затраты второго цикла и т.д.)