Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 11

 – получили межвременное бюджетное ограничение в номинальных показателях, приведенное ко второму периоду.

Поделим всё на  , получим

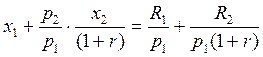
Вспомним определение инфляции: 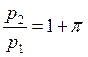  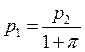, подставляя получаем:

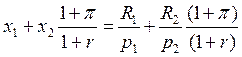
Теперь перейдём к реальным показателям: 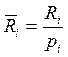 и   

Совсем знакомые и любимые из макры вещи получаются

Решаем задачу:

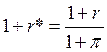
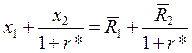
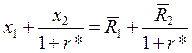
Получаем.

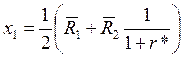                     и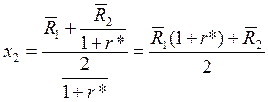            

То есть в каждый год индивид тратит половину приведенного к этому году общего дохода.

Модель общего равновесия без производства

Таких задач мы в ТИГРОРе гору решали, и ничего принципиально нового лектор не сообщила, поэтому этот пункт пробежим кратенько.

Имеем потребителей, каждый их которых решает задачу:

        

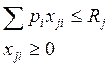
При общих ограничениях на ресурсы (или балансовых ограничениях).

           

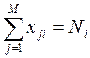
Целью решения данной задачи является поиск оптимальных цен, при которых выполнены балансовые ограничения. Решая свою задачу, каждый из потребителей приходит к условию:

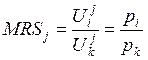
А так как цены в экономике одни и те же, тогда приходим к условию равновесия в модели без производства:

     

Моделирование сферы производства

В данной теме мы считаем спрос потребителей заданным и рассматриваем поведение производителя, максимизирующего свои выгоды.

Под производством понимается процесс взаимодействия экономических факторов, завершаемый выпуском какой-либо продукции. Правила, предписывающие определенный порядок взаимодействия экономических факторов, составляют способ производства или иначе технологию производства. Производство можно представить как систему "затраты-выпуск", в которой выпуском является то, что фактически произведено, а затратами - то, что потребляется в процессе производства (капитал, труд, энергия, сырье). Поэтому формально можно сказать, что производство - это функция, которая каждому набору затрат ставит в соответствие определенный выпуск. Именно такое упрощенное понимание производства как "черного ящика" заложено в математической модели производства. Во "вход" этого черного ящика подаются затраты, а на "выходе" получаем выпуск.

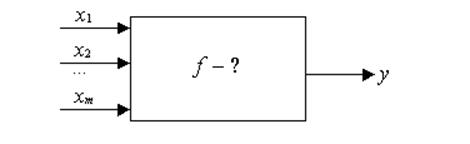
Пусть  – вектор столбец затрат ресурсов, а  – вектор выпуска продукции. И ресурсы, и выпуск предполагаются неотрицательными.

 – производственная функция, характеризующая максимально возможные объёмы производства продуктов при определённых затратах ресурсов.

Заметим, что производственная функция определяется однозначно, это нечто конкретное в отличие от функции полезности.

Сформулируем основные аксиомы, касающиеся производственной функции.

Аксиомы:

1.  Монотонность. Существует подмножество ресурсного множества, называемое экономической областью, в котором большим либо равным затратам ресурса не может соответствовать меньший выпуск, то есть с ростом затрат выпуск по крайней мере не падает. То же проще: если , то . Отсюда следует, что все предельные продукты неотрицательны: .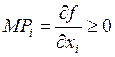

2.  Законом убывающей отдачи. Существует выпуклое подмножество экономической области, для которого выполнено 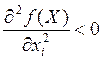. Это условие показывает, что увеличение затрат одного ресурса (при постоянном уровне затрат других ресурсов) приводит к меньшему приросту выпуска.

3.  Поведение в начале координат: .  Результатом бездеятельности является нулевой выпуск. Эта аксиома носит название «отсутствие рога изобилия».

4.  Однородность:  – это означает, что увеличение всех затрат в  раз приводит к увеличению выпуска в  раз. Показатель степени однородности n характеризует изменение эффективности производства при изменении затрат. Возможны три случая.

·   – снижающаяся эффективность производства;

·   – постоянная эффективность производства;

·   – возрастающая эффективность производства.

Предельный анализ и анализ эластичностей в производстве

Эффективность использования ресурсов характеризуется следующими показателями.

Средний продукт: .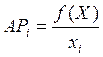

Предельный продукт: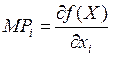  

Эластичность выпуска от затрат: 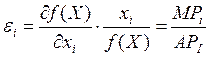. Данный коэффициент показывает предельное отношение относительного прироста производства к относительному приросту затрат.