Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 4

II этап: рассмотрим взаимодействующую систему, систему, где индивиды могут обмениваться.

   где     и

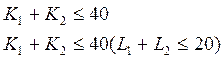
Найдём субоптимальные решения (т.е. решения при которых все ресурсы находятся у одной из подсистем): =40.

Рассмотрим графическое представление нашей задачи:

AD – множество эффективных по Парето ВС – ядро экономической системы, на варианты находящие в этом ядре согласятся оба индивида

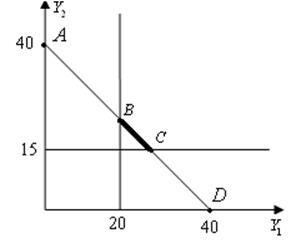
III этап: проблема выбора в ядре, поиск компромиссных цен.

Пусть  - вектор цен. Причём каждая страна стремится иметь неотрицательный торговый баланс – .

Пусть первый регион хочет (ну, мало ли захотелось ему вдруг) производить 21 единицу товара Y. Для этого ему необходимо K=21 и L=10,5 (а у него имеется K=25, L=10), то есть данному региону необходимо продать 4 единицы капитала и закупить 0,5 единиц труда, при этом вывести на равенство свой торговый баланс.

Взаимные задачи. Критерий минимизации издержек.

Для начала, не стоит путать взаимные и двойственные задачи. Взаимные задачи заданы на одном множестве переменных с исходными, а для двойственных мы вводим двойственный.

Рассмотрим Задачу A:

Множество допустимых значений X обозначим  – . А за  – обозначим множество, образованное из , исключением  условия

         

                    

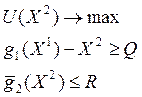
Из множества видов ресурсов выделим дефицитные ресурсы (один или несколько). Ресурс называется дефицитным, если изменение его количества приводит к изменению оптимального значения целевой функции. Всякий дефицитный ресурс (к примеру ) в оптимальном плане X* используется полностью, т.е. вектор X* обращает неравенство  в строгое равенство. Но понятие «дефицитность ресурса» гораздо более жесткое, чем понятие «полное использование ресурса», так как последнее не означает, что увеличение ресурса обязательно изменит оптимальный план (может просто так получилось, что ограничение по какому-либо ресурсу вышло на равенство, однако если ресурс не дефицитен, не факт, что если он нам станет доступен в большем объёме, то мы увеличим его потребление).

Количество дефицитного ресурса L можно рассматривать как параметр, определяющий множество допустимых вариантов . При этом  можно представить как пресечение множества и множество таких вариантов, для которых выполнено , а именно

Теперь сформулируем другую задачу.

Пусть C – параметр, характеризующий определённый уровень максимизируемой  целевой функции . При некотором уровне целевой функции мы пытаемся минимизировать затраты дефицитного ресурса:

Задача B:

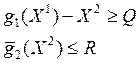
Обозначим за  множество допустимых вариантов данной задачи, которое является пересечением  и множество таких вариантов, для которых выполнено :

Таким образом, имеем пару оптимизационных задач:

Задача А)     ,

Задача B)      , 

Задачи A и B являются взаимными. Как было показано, эти задачи имеют общую часть множества допустимых решений , а различия между ними сводятся к следующему: функция , максимизируемая в задаче A, образует ограничивающее условие в задаче B, и наоборот, функция , минимизируемая в задаче B, образует ограничивающее условие в задаче A.

Пусть вариант  является оптимальным в задаче A, причем таких оптимальных решений может быть несколько. Обозначим множество оптимальных планов как – , то есть .

Теперь рассмотрим вариант  - оптимальное решение задачи B. Множество таких оптимальных решений обозначим , получим .

Первая теорема взаимности:

Если для каждого решения  задачи A, выполняется условие  и в задаче  B, в качестве ограничивающего параметра C, выбрано С*=, то решения задач A и B совпадают.

Док-во (для любителей):

Разобьем доказательство на пункты:

1.  если , то , так как

если , то , так как

2.  Всякое  принадлежит :

     

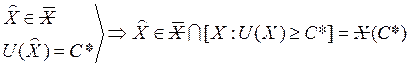
3.  Так как оптимум в задаче B на множестве , то для любого  , в том числе и для , выполнено , то есть

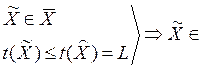
4.  Так  как  максимум  функции  на множестве , то , но , то , следовательно . Теперь мы показали, что ограничение во второй задаче выполняется как строгое равенство, кроме того, последнее равенство означает, что  оптимален в задаче A.