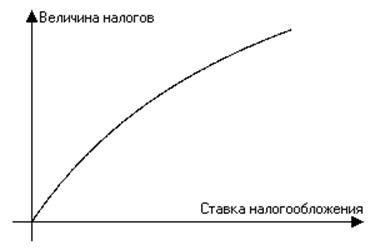
Что касается государства, то его основной задачей в области налогов является определение оптимальной налоговой ставки. Известно, что при высокой ставке налога резко снижается деловая активность фирм и населения в целом (или, как сказал бы Баранов, «снижаются стимулы к бизнесу и труду»). Теоретически эту мысль выразил американский экономист Лаффер. Графически так называемый эффект Лаффера отображается кривой, которая показывает зависимость поступаемых в бюджет сумм налогов от величины ставок налогообложения.
|
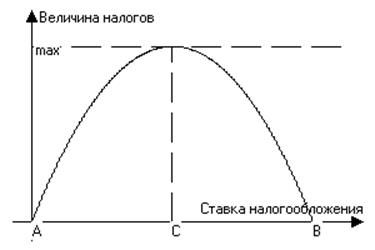
Теперь вернёмся к нашему случаю прямого пропорционального налогообложения. Величина поступлений в бюджет может быть записана следующим образом:
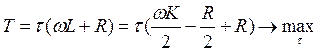
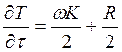
Видим, что величина налоговых поступлений не зависит от налоговой ставки. В данном случае можно сказать, что нет эффекта Лаффера.
Рассчитаем теперь величину поступлений в бюджет при косвенном налогообложении:
Напомню, бюджетное ограничение индивида выглядит следующим образом.
![]() , соответственно
, соответственно
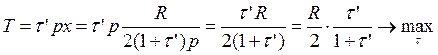
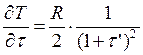 – в данном случае эффект Лаффера также
отсутствует, так как производная строго больше нуля, функция всюду возрастает
и не имеет экстремумов.
– в данном случае эффект Лаффера также
отсутствует, так как производная строго больше нуля, функция всюду возрастает
и не имеет экстремумов.
Прямое прогрессивное налогообложение
Как уже
говорилось, налог является прогрессивным, если с ростом дохода средняя ставка
налога растёт. Самым простым случаем прогрессивного налога является налог с
постоянной предельной ставкой ![]() и гарантированным
доходом (необлагаемым налогом минимумом).
и гарантированным
доходом (необлагаемым налогом минимумом).
Упражнение: убедится, что это действительно прогрессивный налог.
Итак, имеем следующую задачу:
|
![]()
![]()
Если мы, как и ранее перепишем бюджетное ограничение через свободное время и в качестве целевой функции выберем функцию Кобба-Дугласа. То задача перепишется следующим образом:
![]()
![]()
![]()
Решая эту задачу, найдём оптимальное количество свободно времени
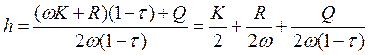 , учитывая, что
, учитывая, что ![]() ,
можно написать
,
можно написать
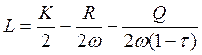
Глядя на эту функцию предложения труда, можно сделать ряд фундаментальных выводов:
· Чем больше ставка налогообложения, тем меньше предложение труда;
· Чем больше заработная плата, тем больше предложение труда;
· Чем больше дотации и необлагаемый налогом минимум (Q), тем меньше предложение труда.
Теперь посмотрим на поступление в государственный бюджет при данной системе налогообложения.
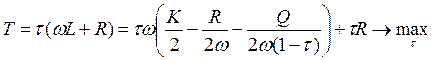
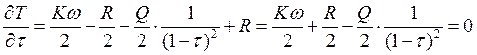
![]()
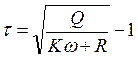
Для полноты картины, стоит проверить, что это точка максимума, а не минимума, поэтому возьмем вторую производную:
 при
при ![]() , то
есть в данной точке действительно достигается максимум.
, то
есть в данной точке действительно достигается максимум.
Теория перманентного дохода Милтона Фридмана
Эта теория исходит из того, что в различные периоды жизни индивида, его доход различен, однако, индивид старается, чтобы его потребление в течение всей жизни было примерно на одном уровне. То есть в период высоких доходов индивид вынужден сберегать денежные средства, чтобы потребить их в период низких доходов. В развитой версии этой теории выделяют четыре периода жизни индивида:
1. учёба, в этот период индивид не имеет дохода и вынужден брать кредит;
2. работа, возврат кредита;
3. пик карьеры, в этот период наиболее крупные сбережения;
4. пенсия, у индивида нет дохода, он живёт на свои сбережения.
Однако мы рассмотрим двухпериодную версию этой модели. Считая, что в первый период индивид имеет больший доход, чем во второй.
Пусть ![]() потребление индивида в первый период,
потребление индивида в первый период, ![]() – во второй;
– во второй; ![]() ,
,![]() – доходы в соответствующие периоды;
– доходы в соответствующие периоды; ![]() – сбережения;
– сбережения; ![]() –
ставка процента в экономике. Кроме того, предположим, что предпочтения
индивида, относительно распределения потребления между двумя периодами заданы
функцией Кобба-Дугласа. Тогда имеем следующую задачу:
–
ставка процента в экономике. Кроме того, предположим, что предпочтения
индивида, относительно распределения потребления между двумя периодами заданы
функцией Кобба-Дугласа. Тогда имеем следующую задачу:
![]()
![]() – бюджетное ограничение
в первый период
– бюджетное ограничение
в первый период
![]() – бюджетное ограничение во второй
период
– бюджетное ограничение во второй
период
![]()
Сведём два бюджетных ограничения в одно:
![]()
![]() , преобразовываем
, преобразовываем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.