Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 3

f(X₁) → max

g¹(X₁) = b¹

Как мы уже выяснили необходимым условием максимума f(X) в задаче такого типа является равенство нулю частных производных функции Лагранжа.

В соответствии с поставленным вопросом (как изменяется целевая функция при изменении вектора b) представим векторы X₁ и Y₁  в виде функций от параметров b¹:

X₁ = X₁(b¹); Y₁ = Y₁(b¹). Функцию Лагранжа также будем рассматривать как дифференцируемую функцию от b¹:

L(b¹) = f[X (b¹)] + Y₁(b¹){b¹ – g[X (b¹)]}

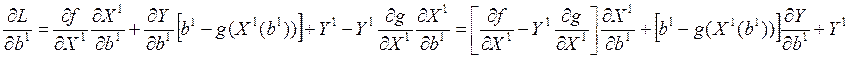
В точке максимума (X*, Y*), из

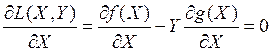
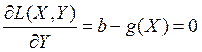
следует, что

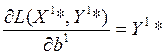
Кроме того,  =, следовательно

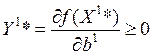
Из условий дополняющей нежесткости следует, что если

 то , тогда имеем

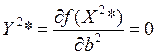
Итак, получим

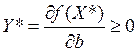 Что и требовалось доказать.

Модели общего равновесия. Модели экономического взаимодействия.

Речь пойдет в основном о равновесии по Вальрасу.

В данной теме мы рассматриваем не унитарную экономику с единой целевой функцией и действующую как единое целое, а федеративную экономику. Под федеративной экономикой понимается некая система взаимосвязанных субъектов, где, однако каждый субъект самостоятельно принимает решения о проводимой экономической политике и существует некое начальное распределение ресурсов.

Итак, пусть у нас есть k подсистем какой-либо системы (k субъектов Российской Федерации). Для каждой такой подсистемы мы имеем задачу:

               где  k=1,…,m

Как вариант решения такой задачи, найти оптимальные решения для каждой из k  подсистем (локальные оптимумы). Однако они, как правило, несовместны (т.е. оптимальное решение для одной подсистемы не является таковым для другой). Это выражается в невыполнении общесистемных ограничений при объединении решений подсистем. Кроме того, система, как правила обладает свойством эмерджентности (синергизма). То есть система теряет некий положительный эффект при разделении её на невзаимосвязанные части. Значит, наша задача состоит в том, чтобы найти оптимальный план для всей системы.

Предположим также, что системы имеют возможность обмениваться ресурсами: - вектор обменов.

Кроме того, должны быть выполнены общесистемные ограничения:

                

Лирическое отступление: поговорим об интеграции.

Стадии интеграционных объединений:

1.  Свободные экономические зоны

2.  Таможенный союз

3.  Общий рынок

4.  Монетарный союз – единая условная денежная единица

5.  Экономический союз

Попытаемся свести  имеющихся у нас k задач в одну:

         где   - вектор функция

 

Кроме того, пусть, если субъект не объединяется в федерацию, а действует обособленно, ему доступен некий уровень целевой функции , тогда в систему следует ввести еще одно условие:

 

Иначе субъект не захочет объединяться в систему.

Для решения получившейся системы в первую очередь необходимо скаляризовать целевую функцию:

       

Если в качестве вектора λ взять орт, то мы получим субоптимальное решение, то есть узнаем, сколько бы мог производить отдельный регион, если бы все ресурсы экономики находились в его распоряжении. Меняя таким образом λ мы получим различные эффективные по Парето решения. Однако это будет довольно широкое множество выбора. Чтобы его сузить ищут ядровые решения.

Ядро – подмножество множества эффективных решений, при которых субъектам экономики выгодно взаимодействовать и не возникает блокирующих коалиций. (Множество дележей не блокируемых не одной коалицией).

Для понимания сущности введенных выше понятий рассмотрим

Пример:

Есть две полсистемы – к примеру, Россия и Украина – которые решают: как быть с Черноморским флотом.

Пусть  – выпуск k-ой подсистемы, где k=1,2. Причем функция выпуска Леонтьевского типа (жесткий комплект):

 –Например, на два корабля нужна сотня моряков. Кроме того, в экономике задано начальное распределение ресурсов.

Имеем следующие задачи:

Общие ресурсные ограничения:

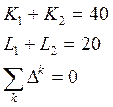
I этап решения: найдем какого уровня выпуска может достичь каждая из под систем при начальном распределении ресурсов, не вступая в коалицию с другой подсистемой, то есть

- в избытке  - в дефиците =20,

- в дефиците  - в избытке =15,  =7.5