Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 8

То есть в первом  случае мы максимизируем функцию полезности при заданном уровне расходов, а во втором случае минимизируем расходы при заданном уровне полезности.

Решая задачу A, мы получаем некий оптимальный , такой что . Но при другом соотношении цен и дохода этот оптимальный вектор будет другим. Однако можно в общем виде попытаться выразить решение этой задач через R  и p. Это будет спрос потребителя при фиксированном уровне затрат, или еще его называют некомпенсированным (или Маршаллианским) спросом. Теперь подставив такое выражение  в целевую функцию, мы получим так называемую косвенную (непрямую) функция полезности – ,  которая показывает каким будет оптимальное значение целевой функции при различных сочетаниях цен и дохода.

Аналогично для задачи B, решая её, мы находим вектор h, который то же можно представить в общем виде через цены и минимально допустимый уровень полезности  – это функция Хиксианского или компенсированного спроса, то есть спрос при заданном уровне полезности. Подставляя это выражение в целевую функцию задачи B, получим  – функция, показывающая минимальный уровень расхода, необходимый для заданного уровня полезности при данных ценах.

В этих терминах первую теорему взаимности можно переформулировать следующим образом: Если , тогда .

Лемма Шепарда:

Движение функции расходов по i-ой цене есть Хиксианский спрос на i-ый товар, то есть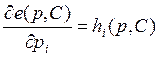

Док-во:

Собственно говоря, по правилу дифференцирования сложной функции:

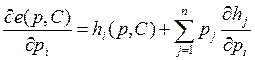
Нам нужно доказать, что 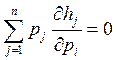, для этого

Рассмотрим  Лагранжиан в задаче B: . Берём дифференциал по переменной :

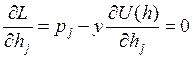 при , из условия дополняющей нежесткости

т.е.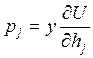 

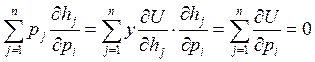
Так как функция полезности как такова не зависит от цен.

Таким образом, мы доказали что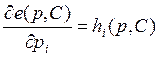

Тождество Роя:

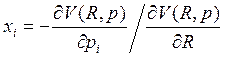 – зная косвенную функцию полезности, можно определить спрос.

Док-во:

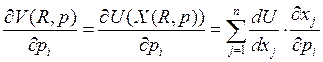
Лагранжиан в задаче A: , дифференцируем

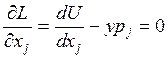 для   (из условия дополняющей нежесткости)  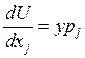  , подставляем

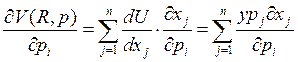
Теперь обратим наш взор на бюджетное ограничение 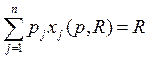 и возьмем производную по , от обеих частей этого выражения, получим

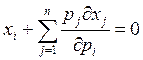 или 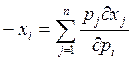      , подставляем

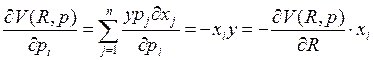
Последнее равенство основывается на свойстве двойственных переменных. Переменная  показывает, на сколько изменится целевая функция, при изменении дохода на единицу.

Выражая , получаем требуемое утверждение:

 

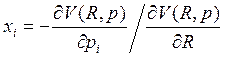
Уравнение Слуцкого

Уравнение Слуцкого выглядит следующим образом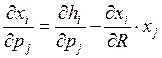

Док-во:

Итак, вспомним историю наших  предшествующих рассуждений. Сначала мы решили задачу максимизации полезности при заданном бюджетном ограничении и получили функцию некомпенсированного спроса потребителя. Затем мы решили задачу минимизации расходов при заданном уровне  полезности и получили функцию компенсированного спроса. Затем из теоремы взаимности мы получили следующее соотношение:

 – величина Маршалианского и Хиксианского спроса совпадают. Или можно переписать для спроса на i-ый товар

Теперь продифференцируем это уравнение по , Получим

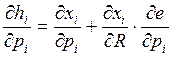 –  из Леммы Шепарда следует, что 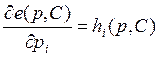, получаем

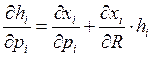 – из теоремы взаимности в точке оптимума, имеем

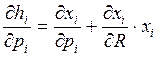 –  преобразовывая, видим

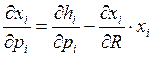, что и требовалось доказать.

Проанализируем данное уравнение:

Величина  отражает изменение в некомпенсированном спросе на i-ое благо, при изменении цены этого блага. Как видно из уравнения оно представляется как сумма двух слагаемых.

 – изменение компенсированного спроса на i-ое благо. Но в компенсированном спросе элиминирован эффект дохода, то есть при любом изменении цен нам компенсируют (доплачивают или отбирают) доход на такую величину, чтобы мы остались на том же уровне полезности. То есть изменение компенсированного дохода в точности отражает эффект замены.

Вторая величина 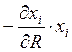 в чистом виде представляет эффект дохода, вызванный изменением цены i-ого блага.

Иногда уравнение Слуцкого переписывают в несколько других обозначениях.

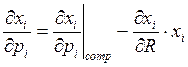
Однако мы будем рассматривать уравнение Слуцкого в более содержательных обозначениях.

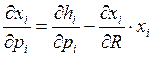
Предположим, что цена блага повышается. Тогда в результате действия эффекта замещения, потребитель сократит потребление этого блага,  заменяя его другими относительно более дешевыми. Следовательно эффект замещения будет всегда иметь отрицательный знак. За эффект замены у нас отвечает первое слагаемое, т.е.