Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 23

В модели Межотраслевого баланса делается существенное (и довольно сильное) предположение о существовании прямой пропорциональной зависимости между объёмами промежуточного потребления и валового выпуска, т.е.

 или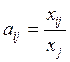

Коэффициент  называют коэффициентом прямых затрат продукции i на производство продукции j. Эти коэффициенты в совокупности образуют квадратную матрицу:

 – которая в свою очередь носит название матрицы прямых затрат.

Тогда формула (1) преобразуются следующим образом:

,  где  i = 1,…,n    или

, где   – символ Кронекера.

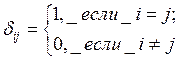
То же самое можно переписать в матричной форме:

   или 

Где  – вектор-столбец объёмов производства;  – вектор-столбец конечной продукции; E  – единичная матрица порядка n.

Видим, что переменных в системе 2n, а уравнений n. Вообще говоря, данная система может иметь единственное решение, если число неизвестных не превышает числа уравнений. Поэтому часть параметров можно зафиксировать, а остальные определять по модели. Принятие одних величин за известные, а других – за  неизвестные определяется постановкой конкретной  экономической задачи. В качестве примеров задач можно рассмотреть: Определение объёмов производства по данным об объёме спроса на конечную продукцию (все  считаются известными, а  переменными). Определение конечной продукции по данным об объёмах производства (считаются известными,  а  переменными). Определение объёмов продукции по одним видам продукции и конечной продукции по другим видам (часть  и  задаются, а часть считаются переменными).

Свойства матрицы прямых затрат,

матрицы A:

·  Матрица коэффициентов прямых затрат должна содержать только неотрицательные элементы  . Такие матрицы называются неотрицательными.

·  Диагональные элементы матрицы А должны быть меньше единицы (). В противном случае производство лишается всякого смысла. То есть при производстве единицы продукции мы должны затрачивать, по крайней мере, меньше единицы того продукта, который производим.

Эти естественные свойства присущи любой матрице прямых затрат, перед тем как разобраться особыми свойствами этой матрицы, определимся с необходимыми нам понятиями из курса линейной алгебры.

Матрицы A и  называются подобными, если . Подобные матрицы имеют равные по величине собственные числа и главные миноры.

Понятие о разложимых и неразложимых матрицах. В теории матриц разложимыми называют такие матрицы A, которые одновременной перестановкой строк и столбцов можно привести к виду:

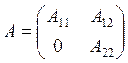
Матрица A неразложима, если для неё не существует таких одновременных перестановок сток и столбцов, которые приводили бы её к разложимой форме. Если матрица прямых затрат A неразложима, то каждая отрасль непосредственно или косвенно расходуется так же при производстве продукции всех других отраслей.

Так теперь, разобравшись с чисто математическими определениями, займемся определениями скорее экономическими.

Продуктивность матрицы A

Если реальная экономическая система характеризуется способностью к непрерывному воспроизводству, то матрица A должна иметь особый вид, который обеспечивает возможность получить конечный продукт при соответствующих пропорциях развития производства.

Матрица A продуктивна, если существует такой неотрицательный вектор выпуска , который обеспечивает положительный по каждой компоненте вектор конечного потребления . Неразложимая матрица A  продуктивна, если существует такой , что

Для конкретного практического межотраслевого баланса (в котором всегда X>0) свойство продуктивности проверяется очень просто: если , то система продуктивна. Однако если это условие не выполнено, т.е. , то из этого еще нельзя сделать вывод о непродуктивности матрицы A. Можно, взяв вместо неположительных компонент вектора Y положительные значения, рассчитать новые значения X. И если при этом оказывается, что ,  то матрица A  продуктивна.