Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 5

5.  То есть , или, что то же самое,             (*)

любой оптимальный вектор задачи B является оптимальным и в задаче A. Но для каждого оптимального вектора в задаче A  ресурсное ограничение выполнено на равенство, значит =min.

6.  Так как  выполнено (пункт 2.) и  min=L=  ,  а значит                 (**)

Из выражений (*) и (**) следует, что = Что и требовалось доказать!!!

Вторая теорема взаимности:

Пусть  двойственная переменная (множитель Лагранжа) для ограничения  задачи A, а  двойственная переменная для ограничения  в задаче B. Тогда  и  обратно пропорциональны, а все остальные двойственные переменные взаимных задач пропорциональны с коэффициентом пропорциональности  (или ) .

Как доказывается эта теорема я не знаю :(( Зато можно посмотреть логически:

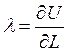 – показывает, на сколько изменится целевая функция,  при изменении затрат на единицу.

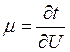– показывает, на сколько изменятся затраты при изменении требуемого уровня целевой функции на единицу.

То есть, даже из содержательной интерпретации двойственных переменных можно сделать вывод, что это обратные показатели.

Модели частичного равновесия

Модель поведения потребителя

В общем виде задача потребителя записывается следующем образом

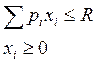
Основные  ы потребительских предпочтений:

1.  Аксиома сравнимости: между любыми двумя векторами возможно одно из следующих предпочтений:

 , или

2.  Аксиома транзитивности: если  и , то

3.  Аксиома непрерывности: если  и , то , такое что (да, это не та аксиома непрерывности, что нам давали в ТИГРОРе, но времена меняются…)

4.  Аксиома ненасыщенности  (монотонности): если , то либо , либо , причём если  и , то . По сути, эта аксиома означает, что оба блага полезны для потребителя, поэтому он предпочтёт  набор с большим количеством какого-либо блага, при одинаковом количестве остальных благ.

5.  Аксиома строгой выпуклости: если  и , то и

Графическая иллюстрация:

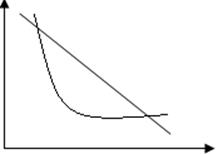
В данном курсе рассматриваются только предпочтения заданные целевой функцией, с такими предпочтениями удобней работать, и именно для них разработана теория математического моделирования. Однако не стоит забывать, что ни один индивид не может точно назвать свою целевую функцию, хотя свои предпочтения довольно однозначно, могут определить большинство индивидов.

Итак, целевая функция . Стоит, однако, заметить, что эта функция определяется неоднозначно, с точностью до монотонно возрастающего преобразования . Ряд свойств целевой функции удобно изучать с помощью поверхностей безразличия (если X – двухмерный вектор, то – кривых  безразличия):

, где с – меняющийся параметр, характеризующий уровень целевой функции.

Меняя с можно построить карту кривых безразличия. На одной кривой будут лежать наборы благ, приносящие одинаковый уровень полезности, причем, хотя определение целевой функции неоднозначно, семейство кривых безразличия единственно.

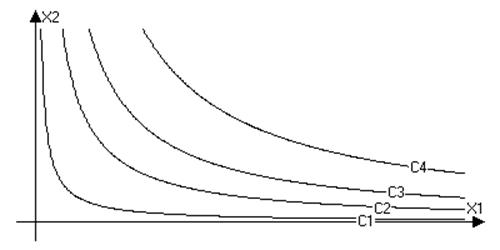Кривые безразличия возрастают по всем своим аргументам (аксиома ненасыщенности), т.е. увеличение потребления одного блага при неизменном уровне потребления всех остальных благ увеличивает значение целевой функции. Поэтому более удаленная от начала координат поверхность соответствует большему значению целевой функции. Тогда  наша задача сводится к нахождению допустимых точек, принадлежащие кривой безразличия, максимально удаленной от начала координат.

Кроме того, стоит заметить, что поверхности безразличия не могут пересекаться, иначе получалось бы, что один и тот же набор соответствует разным уровням полезности, что в принципе невозможно.

Основные виды целевых функций

1.  , где   – функция Кобба-Дугласа, приятной особенностью этой функции является то, что в оптимальном плане не один  не занулится.

2.   – функция Стоуна. Где  , – минимальное количество блага , необходимое для проживания, т.е. как бы отграничили  от нуля.

3.  – линейная функция, характеризует взаимозаменяемые товары.