Целевые установки развития и типы экономических моделей. Модели общего равновесия. Модели экономического взаимодействия. Связь между производственными функциями с взаимозаменяемыми ресурсами и функциями производственных затрат, страница 20

, где s₂M₂   – вектор-функция затрат ресурсов.

Составим задачу в общем виде:

A) Задача потребителя

– доля k-ого индивида в прибыли l-ого предприятия

  

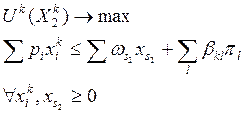
B) Задача производителя (фирмы)

Q – вектор фиксированного потребления  – вектор запаса невоспроизводимых ресурсов

С) Общесистемные ограничения

   –     спрос = предложению

 

Ищем частные решения в каждом из выше перечисленных пунктов. В итоге оптимальное решение должно удовлетворять следующим условиям:

        – для одноименных товаров предельные нормы замещения для каждого потребителя равны.

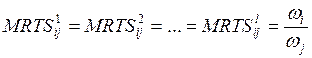 – для одноименных ресурсов предельные нормы технического замещения равны для каждого предприятия и равны соотношению цен этих ресурсов.

 – придельные нормы трансформации всех ресурсов совпадают.

Теперь всё-таки определим эти показатели (по крайней мере, в этом курсе они определяются так):

1. 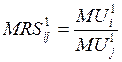 – предельная норма замещения равна отношению предельных полезностей благ i и j для первого потребителя.

2. 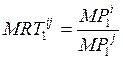– предельная норма трансформации равна отношению предельных продуктов по первому ресурсу на предприятиях i и j.

3. 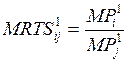 – предельная норма технического замещения равна отношению предельных продуктов ресурсов i и jна первом предприятии.

Как уже отмечалась (в первой части лекций), данная задача может быть скаляризованна следующим образом:

 – общий объём выпуска;

 – общий объём потребления;

 – общий объём затрат ресурсов.

 – целевой функции каждого индивида сопоставили вес, с которым она вошла в общую целевую функцию.

Тогда задача перепишется следующим образом:

Задача в такой постановке называется моделью Бентама

Аналогами цен в данной модели выступают двойственные переменные, которые обозначаются для первой группы неравенств , а для второй группы неравенств .

Анализ производственных способов. Общая линейная оптимизационная модель.

Производственный способ – это некоторое соотношение различных видов затрат и выпуска продукции. Это понятие с одной стороны является конкретизацией понятия «вид деятельности», с другой стороны – это некоторое обобщение функций затрат. Пусть мы имеем N способов производства, .

Интенсивность применения способа  будем обозначать, как , эта интенсивность может измеряться объёмом какого-либо выпускаемого продукта или объёмом какого-либо затрачиваемого ресурса. Каждому способу  соответствует вектор , компонентами которого являются коэффициенты выпуска продукции (со знаком «плюс») и затраты различных видов ресурсов (со знаком «минус»). Очевидно, невозможно произвести какой-либо продукт, не затратив никаких других продуктов или ресурсов; с другой стороны способы, в которых ничего не производятся, также абсурдны. Поэтому в каждом векторе  обязательно содержатся как положительные, так и отрицательные компоненты.

Совокупность производственных способов образует матрицу .

Как правило, в производстве могут одновременно применяются несколько способов (свойство аддитивности). При этом обычно предполагается, что характеристики одного способа не зависят от применения других способов (свойство автономности). То есть линейная комбинация базовых способов образует новый способ. Например, если  – базовые способы, тогда 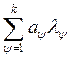, где  и , даёт новый способ.

Как и ранее разобьём множество всех ингредиентов на два подмножества: продукты  и не воспроизводимые ресурсы . Тогда  характеризует выпуск конечной продукции, а   – общие затраты не воспроизводимого ресурса.

Обозначим  – требуемый объём конечной продукции вида , а  – наличные ресурсы вида . Тогда можно записать следующие основные ограничения линейной модели производства:

первая группа ограничений – ограничения по продуктам; вторая группа ограничений – ограничения по ресурсам

      

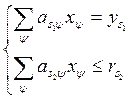
Анализ однопродуктовых способов