Вероятностное описание погрешностей измерения

ВЕРОЯТНОСТНОЕ ОПИСАНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ

В измерительной технике имеют дело с большим количеством массовых явлений. Сюда относится множество измерений, проводимых с помощью одного и того же средства измерений (СИ), характеристики множества СИ одинакового типа и т.д. При этом мы встречаемся как со случайными событиями (отказы СИ, правильные и неправильные решения при контроле, наличие грубых промахов), так и со случайными величинами (погрешности измерения, время безотказной работы, значение контролируемого параметра) и случайными процессами (флуктуации питающих напряжений, тепловые и дробовые шумы электронных устройств). В силу этого аппарат теории вероятностей оказывается наиболее адекватным сути многих задач измерительной техники.

1. Случайные события и их вероятности

Понятие о случайном событии является одним из исходных в теории ве­роятностей (ТВ). Некоторое событие  называется случайным, если при выполнении определенных, заранее оговоренных условий оно может произойти или не произойти. Примеры: выигрыш в лотерее (заранее оговоренные условия: необходимо сначала купить лотерейный билет, а потом выигрыш может быть, а может – нет), бросание игральной кости и т.д. В измерительных задачах: пребывание погрешности измерения в определенном интервале, различные ошибки контроля.

Антиподами случайного события являются детерминированные события, которые включают в себя достоверные и невозможные события. (Придумайте примеры самостоятельно).

Достоверным событием  называется такое, которое обязательно произойдет при выполнении некоторого комплекса условий. Событие  называется невозможным, если при заранее оговоренных условиях оно не может произойти. (Придумайте примеры самостоятельно).

Существует два подхода к определению вероятности случайного события: статистический и классический.

Статистическое определение вероятности. Пусть при одинаковых условиях проводится серия  независимых испытаний, и в  опытах произошло случайное событие . В результате многократных наблюдений экспериментально установлен закон, заключающийся в том, что относительная частота появления события

                                                   (1.1)

незначительно изменяется от серии к серии. Причем это отличие с среднем уменьшается с ростом . Такой эмпирический закон положен в основу статистического определения вероятности.

Вероятностью события  называется число , вокруг которого группируются значения относительной частоты появления этого события.

Недостаток этого определения состоит в том, что оно не указывает, каким способом найти это число . Практически при экспериментальном определении вероятности предполагают, что

.                                                     (1.2)

Поскольку с ростом числа опытов  разброс  уменьшается, напрашивается более строгое определение вероятности как предела

.

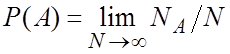Но в этом случае предел в том смысле, как его понимают в математическом анализе, не существует. Подробнее об этом можно прочитать у Гнеденко.

Классическое определение вероятности. Оно более строгое с математической точки зрения.

Пусть в результате эксперимента обязательно происходит одно и только одно из равновозможных событий  , а к событию  приводят только  событий из . Тогда вероятностью события  называется отношение

.                                                (1.3)

Пример 1. Пусть бросается игральная кость, а событие  заключается в том, что цифра на верхней грани делится на . Найти .

, , из (1.3) .                                

Существует ещё более строгое аксиоматическое определение, данное академиком Колмогоровым, но оно здесь не приводится, поскольку подразумевает знание изучающим теорию вероятностей основ функционального анализа.

Поскольку строгое определение вероятности затрудняет его практическое применение из-за сложности определения равновозможных исходов, то в прикладных задачах, как правило, пользуются в неявном виде статистическим определением.

Из всех определений вероятности следует:

; ; .                                   

Вероятность произведения случайных событий. Событие , заключающееся в появлении в одном эксперименте одновременно всех событий , называется произведением этих событий:

.                                                     

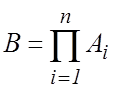Пример со стрельбой биатлониста. Биатлонист подъехал к огневому рубежу. Допустим, что событие A_i заключается в том, что биатлонист своим i-м выстрелом разобьёт i-ю тарелочку. А событие B заключается в том, что с огневого рубежа биатлонист уйдёт без штрафа (разобьёт все тарелочки). В этом случае событие B произойдёт только тогда, когда одновременно произойдут все события . При этом, если говорить о вероятностях поражения биатлонистом мишеней, то при стрельбе по i-й мишени будет рассматриваться вероятность её поражения при условии, что все предыдущие мишени были поражены.

Поэтому в ТВ рассматривают условные вероятности. Вероятность появления события  при условии, что событие  уже произошло, называется условной вероятностью и обозначается . Вероятность события  в случае, когда , равна

.                 (1.4)

Если же события  независимы друг от друга, то есть вероятность наступления любого из них никак не зависит от появления или “непоявления” остальных, то формула (1.4) упрощается:

.                                              (1.5)

А в общем случае формулы (1.4), (1.5) примут вид:

,          (1.6)

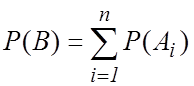.                                              (1.7)

Вероятность суммы случайных несовместных событий. Событие , заключающееся в появлении хотя бы одного из событий , называется суммой этих событий:

.                                                                

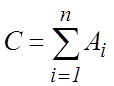События  называются попарно несовместными, если в каждом опыте не могут произойти одновременно любые два из них.

Можно показать, что в этом случае

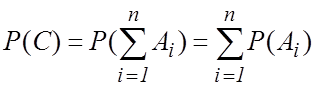.                                    (1.8)

Попарно несовместные события образуют полную группу, если в результате эксперимента обязательно происходит одно из них, то есть

;            ,                                           

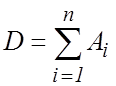тогда

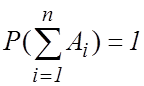.                                                  (1.9)

Событие  называется противоположным, если  и  образуют полную группу событий.

.                                            (1.10)

2. Случайные величины и их распределения

Случайные события характеризуют результаты эксперимента с качественной стороны. Гораздо чаще целью эксперимента является определение размера некоторой физической величины. Именно такие эксперименты составляют предмет любого измерения. По своей физической природе измеряемые величины могут быть детерминированными и случайными.

Будем называть случайной величиной такую величину , которая при выполнении некоторых, заранее оговоренных условий может принимать любое, заранее непредсказуемое значение из некоторого множества значений. Это множество должно содержать не менее двух чисел.

Если величина в ходе эксперимента может принимать только одно значение, то она называется детерминированной.