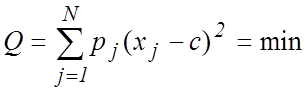 , (2)
, (2)
т.е. при выборе ![]() по предписанию
наименьших квадратов с учетом весов
по предписанию
наименьших квадратов с учетом весов ![]() . Приравнивая
частную производную
. Приравнивая
частную производную ![]() из (2) по
из (2) по ![]() нулю, получаем
нулю, получаем
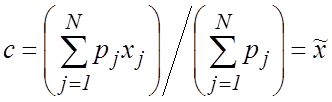 . (3)
. (3)
Оценка ![]() называется средней взвешенной
оценкой. Несложно показать [1,2], что математическое ожидание и дисперсия
оценки
называется средней взвешенной
оценкой. Несложно показать [1,2], что математическое ожидание и дисперсия
оценки ![]() соответственно равны:
соответственно равны:
![]() ;
; 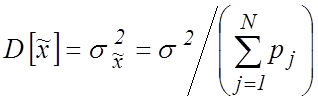 .
.
Таким образом, оценка ![]() является несмещенной, а ее вес равен
сумме весов усредняемых результатов. В [1] показано, что данная оценка эффективна.
является несмещенной, а ее вес равен
сумме весов усредняемых результатов. В [1] показано, что данная оценка эффективна.
Для нахождения оценки
параметра ![]() продифференцируем (1) по
продифференцируем (1) по ![]() и приравняем производную нулю. Из
получающегося уравнения вычисляем:
и приравняем производную нулю. Из
получающегося уравнения вычисляем:
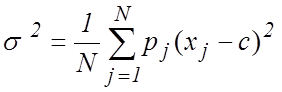 .
.
Аналогично случаю равноточных
измерений вместо ![]() используем его оценку
максимального правдоподобия (3), тогда:
используем его оценку
максимального правдоподобия (3), тогда:
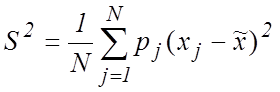 . (4)
. (4)
Оценка является смещенной; для ликвидации ее смещенности вводится поправочный множитель
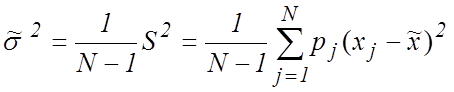 . (5)
. (5)
Построение доверительного
интервала для величины ![]() основано на том, что
величина
основано на том, что
величина
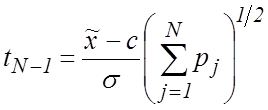
распределена по закону Стьюдента с ![]() степенями
свободы. Поэтому доверительный интервал для истинного значения
степенями
свободы. Поэтому доверительный интервал для истинного значения ![]() будет
будет
![]() , (6)
, (6)
где ![]() – число из таблицы
распределения Стьюдента, соответствующее заданному уровню значимости
– число из таблицы
распределения Стьюдента, соответствующее заданному уровню значимости ![]() и числу степеней свободы
и числу степеней свободы ![]() .
.
Аналогично дробь
![]() ,
,
распределена по закону ![]() с
с ![]() степенями свободы; и доверительным
интервалом для параметра
степенями свободы; и доверительным
интервалом для параметра ![]() будет
будет
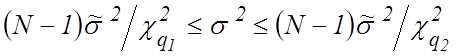 , (7)
, (7)
где ![]() и
и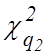 –
числа из таблицы
–
числа из таблицы ![]() -распределения,
соответствующие заданной даверительной вероятности и числу степеней свободы
-распределения,
соответствующие заданной даверительной вероятности и числу степеней свободы![]() .
.
Двенадцать студентов измеряли
сопротивление проводника R одним
и тем же способом. Каждый студент провел различное количество наблюдений,
подсчитал выборочное среднее значение собственных наблюдений ![]() и записал его. Результаты измерений
приведены в таблице 1. Считая отдельные наблюдения всех студентов равноточными
и независимыми, оценить значение сопротивления проводника и точность его
определения, используя результаты измерений выборочного среднего всеми
студентами.
и записал его. Результаты измерений
приведены в таблице 1. Считая отдельные наблюдения всех студентов равноточными
и независимыми, оценить значение сопротивления проводника и точность его
определения, используя результаты измерений выборочного среднего всеми
студентами.
Таблица 1.
|
Номер ст-та j |
Среднее значение сопротивления
|
Число наблюдений
|
Вес измерения
|
|
|
|
1 |
12.208 |
3 |
0.231 |
0.0480 |
0.009994 |
|
2 |
12.476 |
4 |
0.308 |
0.1466 |
0.069785 |
|
3 |
12.193 |
11 |
0.876 |
0.1691 |
0.032630 |
|
4 |
12.306 |
7 |
0.538 |
0.1646 |
0.050376 |
|
5 |
12.691 |
6 |
0.462 |
0.3192 |
0.220596 |
|
6 |
12.794 |
13 |
1.000 |
0.7940 |
0.630436 |
|
7 |
11.660 |
5 |
0.385 |
-0.1309 |
0.044506 |
|
8 |
12.481 |
8 |
0.615 |
0.2958 |
0.142287 |
|
9 |
13.363 |
4 |
0.308 |
0.4198 |
0.572193 |
|
10 |
13.025 |
9 |
0.692 |
0.7093 |
0.727033 |
|
11 |
12.867 |
12 |
0.923 |
0.8002 |
0.693809 |
|
12 |
12.717 |
10 |
0.769 |
0.5707 |
0.395334 |
|
Сумма |
7.107 |
4.3064 |
3.588979 |
Если предположить, что
отдельные наблюдения у всех студентов не имеют систематических погрешностей,
т.е. ошибки измерений распределены по нормальному закону с нулевым
математическим ожиданием и неизвестной дисперсией ![]() ,
то подсчитанные ими средние значения
,
то подсчитанные ими средние значения ![]() будут уже
неравноточными, т.к. студенты провели различное число наблюдений. Поэтому при
расчете оценок неизвестных параметров R и
будут уже
неравноточными, т.к. студенты провели различное число наблюдений. Поэтому при
расчете оценок неизвестных параметров R и ![]() выборочные средние
выборочные средние ![]() должны использоваться с учетом весов
измерений
должны использоваться с учетом весов
измерений ![]() , которые теория рекомендует выбирать
обратно пропорциональными дисперсиям соответствующих погрешностей результатов
измерений. В данном случае в качестве весов можно выбрать значения,
пропорциональные объему выборок
, которые теория рекомендует выбирать
обратно пропорциональными дисперсиям соответствующих погрешностей результатов
измерений. В данном случае в качестве весов можно выбрать значения,
пропорциональные объему выборок ![]() в сериях.
в сериях.
Для удобства расчетов веса
отнормированы к значению максимального из ![]()
![]() , они приведены в таблице в столбце
, они приведены в таблице в столбце ![]() .
.
В данном случае для решения
задачи необходимо воспользоваться результатами раздела 1.1. Оценки неизвестных
параметров R и ![]() находятся из выражений (3)
и (5), но для удобства их вычислений на калькуляторе рекомендуется заменить их
на эквивалентные формулы (3а) и (5а), выбрав надлежащим образом величину
находятся из выражений (3)
и (5), но для удобства их вычислений на калькуляторе рекомендуется заменить их
на эквивалентные формулы (3а) и (5а), выбрав надлежащим образом величину ![]() , например
, например ![]() .
.
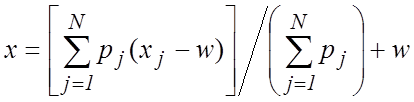 (3a)
(3a)
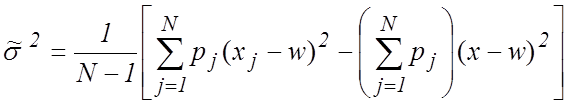 (5a)
(5a)
Из (3a) и (5a) находим ![]() ;
;
![]() ;
; ![]() .
.
Теперь построим доверительные
интервалы для ![]() и
и ![]() .
Выберем доверительную вероятность, равной
.
Выберем доверительную вероятность, равной ![]() ,
тогда для числа степеней свободы
,
тогда для числа степеней свободы ![]() по таблице
распределения Стьюдента находим
по таблице
распределения Стьюдента находим ![]() . Подставляя
значение точечной оценки
. Подставляя
значение точечной оценки ![]() и величины
и величины ![]() в (6), вычисляем
в (6), вычисляем ![]() . Для тех же самых
. Для тех же самых ![]() и
и ![]() по
таблице распределения
по
таблице распределения ![]() находим два числа
находим два числа 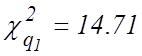 и
и 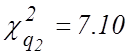 и
подставляем их в (2) (см. Ч.II). Получаем доверительный интервал для
параметра
и
подставляем их в (2) (см. Ч.II). Получаем доверительный интервал для
параметра ![]() :
: ![]() .
Тогда доверительный интервал для
.
Тогда доверительный интервал для ![]() равен:
равен: ![]() .
.
При совместных измерениях неизвестные значения искомых параметров находят из решения системы уравнений, связывающей эти параметры с величинами, измеряемыми непосредственно. Из всего многообразия систем уравнений аналитические решения в общем случае можно выписать только для линейных систем. Поэтому сначала рассмотрим методы обработки экспериментальных данных, когда искомые параметры определяются в результате решения линейных уравнений, а далее проанализируем нелинейный случай.
Пусть имеется линейная система уравнений:
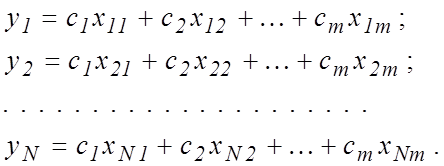
где ![]()
![]() –
искомые неизвестные параметры;
–
искомые неизвестные параметры; ![]()
![]() измеряемые значения величин;
измеряемые значения величин; ![]() – величины, значения которых точно
известны.
– величины, значения которых точно
известны.
Перепишем данную систему в виде
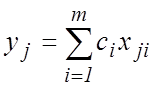 ,
, ![]() . (1)
. (1)
Будем считать, что уравнения
(1) выполняются точно, однако значения ![]() измеряются
с погрешностями, то есть мы наблюдаем искаженные погрешностями величины
измеряются
с погрешностями, то есть мы наблюдаем искаженные погрешностями величины
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.