Вероятностное описание погрешностей измерения, страница 15

Принимая во внимание результаты раздела 1, необходимо найти оценки выборочного среднего  и стандартного отклонения  эквивалентной электропроводности и подставить их в (1). Расчет этих величин производим по формулам (6) и (10) (или (16) и (17), например, выбрав ). Получаем , , . Далее по таблице распределения Стьюдента находим величины , ,  для числа степеней свободы  и уровней значимости ,  и  соответственно. Имеем ; ; .

Для значения  по формуле (1) ; сравнивая его последовательно с , , , видим, что , , . Значит с уровнем значимости  гипотеза о равенстве величине  отвергается, а с уровнями значимости  и  – принимается.

Для значения  по формуле (1) ; в данном случае , , . Значит с уровнями значимости  и  гипотеза о равенстве        величине  отвергается, а с уровнем значимости  – принимается.

Для значения  по формуле (1) ; т.е. , , , и для всех выбранных уровней значимости проверяемая гипотеза отвергается.

Одновременно эквивалентная электропроводность измерялась другим способом, получены следующие результаты:

75.15	72.48	71.68	72.39	72.23	76.61	76.19	71.98	73.22	76.65
72.4		75.15		75.88		75.04		68.36

Для тех же самых уровней значимости проверить гипотезу о равенстве дисперсий определения эквивалентной электропроводности первым и вторым методами.

Для решения поставленной задачи нужно воспользоваться результатами раздела 3, но предварительно необходимо найти оценку дисперсии второго метода. Данную оценку можно получить, вторично применив формулы (6) и (10) (или (16),(17), ). Имеем ,  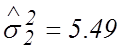число степеней свободы . Теперь составляем -отношение Фишера (3):

                              

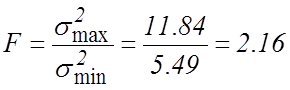
и по таблице распределения Фишера находим числа, соответствующие степеням свободы ,  и уровням значимости ; ;  соответственно: , , . Видим, что , , . Значит с уровнем значимости  гипотеза о равенстве дисперсий должна быть отвергнута, а с уровнями значимости  и  может быть принята.

5.2. Опыты Кэвендиша [1, стр.105]

Английский физик Кэвендиш в 1789 г. опубликовал результаты 29 измерений плотности Земли  (Таблица 1). Предполагая, что измерения равноточны, независимы и принадлежат одной и той же нормальной совокупности с неизвестными  и  , проверить, следует ли отвергнуть значение  как грубую ошибку измерения или нет.

5.50	0.50	0.250	5.34	0.34	0.116
5.61	0.61	0.372	5.99	0.99	0.980
5.88	0.88	0.774	5.10	0.10	0.010
5.07	0.07	0.005	5.27	0.27	0.073
5.26	0.26	0.068	5.39	0.39	0.152
5.55	0.55	0.303	5.42	0.42	0.176
5.36	0.36	0.130	5.47	0.47	0.221
5.29	0.29	0.084	5.63	0.63	0.397
5.58	0.58	0.336	5.34	0.34	0.116
5.65	0.65	0.423	5.46	0.46	0.212
5.57	0.57	0.325	5.30	0.30	0.090
5.53	0.53	0.281	5.75	0.75	0.563
5.62	0.62	0.384	5.68	0.68	0.462
5.29	0.29	0.084	5.85	0.85	0.723
5.44	0.44	0.194
			Сумма	14.19	8.304

Таблица 1.

Для проверки выдвинутой гипотезы составим дробь (4). Неизвестные параметры  и  вычислим по формулам (16), (17), положив . Значения  и 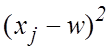 и их суммы приведены в таблице 2. Имеем: ; ; . Тогда . По таблице распределения Грэббса находим, что при  значение  для -го уровня значимости равно . Поскольку  меньше , то  следует оставить как допустимое в данном ряду наблюдений.

ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

1. Точечное оценивание

В практике измерений встречаются ситуации, когда оценки измеряемых величин должны быть получены путем обработки результатов измерений, выполненных в различных условиях: различными экспериментаторами, разными методами, с использованием различных средств измерений. При этом часто нет оснований для того, чтобы отдать исключительное предпочтение какой-либо одной группе результатов, а остальные отбросить как не заслуживающие доверия. В то же время степень доверия тем или иным результатам может быть различна, например, из-за различия в точностях примененных средств измерений.

Таким образом, каждому используемому результату или группе результатов измерений необходимо приписать некоторый вес, характеризующий степени доверия этим результатам.

Обычно веса устанавливаются на основе имеющихся данных о степени неопределенности тех или иных результатов, т.е. обратно пропорциональными дисперсиям соответствующих погрешностей результатов измерений:

,                          

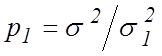где  – вес соответствующий -му результату или -й группе результатов;  – дисперсия соответствующих результатов измерений;  – неизвестный коэффициент пропорциональности, подлежащий оцениванию наряду с измеряемой величиной.

Рассмотрим задачу обработки результатов прямых неравноточных измерений. Пусть даны результаты неравноточных измерений , которые независимы и имеют нормальное распределение с математическим ожиданием  и дисперсиями , причем веса  известны. Необходимо найти оценки измеряемой величины c и параметра .

Плотность распределения любого результата

. 

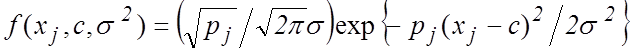Ввиду этого и в силу независимости наблюдений, функция правдоподобия выборки наблюдений  имеет вид

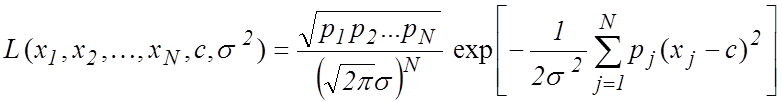.         (1)

Максимум функции правдоподобия достигается при выполнении условия