2)
математическое ожидание
погрешности ![]() , т.е. отсутствует систематическая погрешность;
, т.е. отсутствует систематическая погрешность;
3)
погрешность ![]() имеет дисперсию
имеет дисперсию ![]() , одинаковую для всех измерений, т.е.
измерения равноточные;
, одинаковую для всех измерений, т.е.
измерения равноточные;
4) погрешности отдельных наблюдений независимы.
Тогда
плотность распределения любого результата ![]() запишется
в виде:
запишется
в виде:
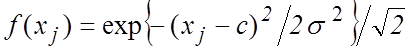 . (2)
. (2)
Так
как результаты отдельных наблюдений независимы, то плотность распределения
системы случайных величин ![]() представляющая
собой функцию правдоподобия выборки, будет иметь вид:
представляющая
собой функцию правдоподобия выборки, будет иметь вид:
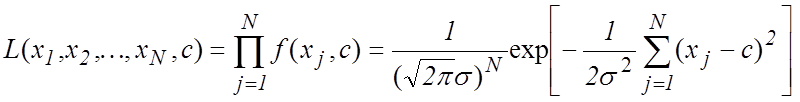 . (3)
. (3)
Найдем
оценку максимального правдоподобия ![]() неизвестного
параметра
неизвестного
параметра ![]() , используя результаты наблюдения
(1). Она выбирается так, чтобы при
, используя результаты наблюдения
(1). Она выбирается так, чтобы при ![]() достигалось
достигалось
![]() . (4)
. (4)
Из (3) следует, что для выполнения (4) необходимо, чтобы
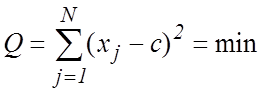 (5)
(5)
Условие
(5) совпадает с критерием наименьших квадратов [1, 2]. Поэтому при
нормальном законе распределения погрешностей наблюдения оценки по ММП и МНК совпадают.
Подставляя в (5) ![]() вместо
вместо ![]() и приравнивая частную производную
и приравнивая частную производную ![]() по
по ![]() нулю,
получаем значение оценки
нулю,
получаем значение оценки ![]() по ММП, которое
совпадает с оценкой
по ММП, которое
совпадает с оценкой ![]() по МНК.
по МНК.
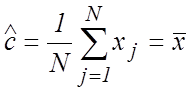 , (6)
, (6)
т.е. наилучшей оценкой является выборочное среднее значение ![]() результатов наблюдений. Из (6)
следует, что оценка
результатов наблюдений. Из (6)
следует, что оценка ![]() является случайной
величиной с нормальным законом распределения, причем
является случайной
величиной с нормальным законом распределения, причем
![]() ;
; 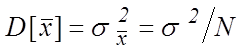 . (7)
. (7)
Таким
образом, оценка ![]() имеет более высокую
точность, т.к. ее дисперсия в
имеет более высокую
точность, т.к. ее дисперсия в ![]() раз меньше
дисперсии отдельных измерений. Разброс результатов оценивания характеризуется
значением среднего квадратического отклонения погрешности, поэтому из (7)
следует, что при усреднении результатов N наблюдений случайная
погрешность уменьшается в
раз меньше
дисперсии отдельных измерений. Разброс результатов оценивания характеризуется
значением среднего квадратического отклонения погрешности, поэтому из (7)
следует, что при усреднении результатов N наблюдений случайная
погрешность уменьшается в ![]() раз. На рис. 1
показаны графики плотностей вероятности исходных наблюдений
раз. На рис. 1
показаны графики плотностей вероятности исходных наблюдений ![]() и выборочного среднего
и выборочного среднего ![]() для
для ![]() . Полученная оценка
. Полученная оценка ![]() является состоятельной, несмещенной
и эффективной.
является состоятельной, несмещенной
и эффективной.
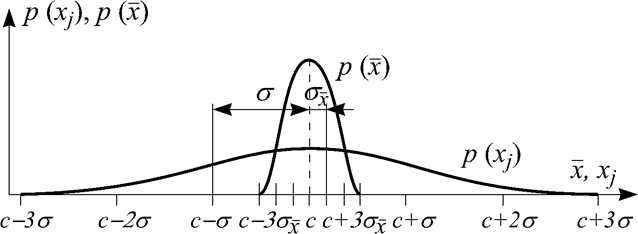
Рис. 1.
Для
оценки неопределенности (разброса) величины с необходимо оценить значение
дисперсии ![]() погрешности измерений. Из (3) видно,
что функция правдоподобия выборки
погрешности измерений. Из (3) видно,
что функция правдоподобия выборки ![]() зависит еще и от
параметра
зависит еще и от
параметра ![]() , поэтому ее можно представить в виде
, поэтому ее можно представить в виде
![]() . Вычисляя частную производную
логарифма этой функции по
. Вычисляя частную производную
логарифма этой функции по ![]() и приравнивая ее
нулю (здесь пользуются свойством монотонности функции логарифм), находим
и приравнивая ее
нулю (здесь пользуются свойством монотонности функции логарифм), находим
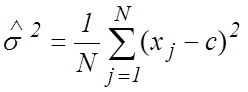 .
(8)
.
(8)
Но
истинное значение c неизвестно, поэтому в (8) вместо ![]() подставляют его оценку максимального
правдоподобия (6), а соответствующую оценку дисперсии обозначим
подставляют его оценку максимального
правдоподобия (6), а соответствующую оценку дисперсии обозначим ![]() :
:
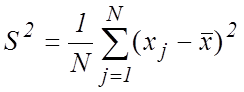 . (9)
. (9)
Однако
доказано, что оценка ![]() , вычисляемая по (9),
получается смещенной [1-4], т.к. ее математическое ожидание не равно
, вычисляемая по (9),
получается смещенной [1-4], т.к. ее математическое ожидание не равно ![]() .
. ![]() .
Но
.
Но 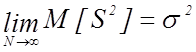 , поэтому оценка
, поэтому оценка ![]() называется асимптотически
несмещенной. Полученную смещенную оценку легко сделать несмещенной, введя поправочный
множитель. Обозначим несмещенную оценку параметра
называется асимптотически
несмещенной. Полученную смещенную оценку легко сделать несмещенной, введя поправочный
множитель. Обозначим несмещенную оценку параметра ![]() через
через
![]() :
:
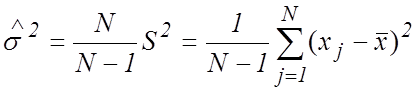 . (10)
. (10)
Существует другая форма записи выражения (10), более удобная в вычислительном отношении при обработке результатов наблюдения на ЭВМ, но уступающая (10) с точки зрения точности вычислений:
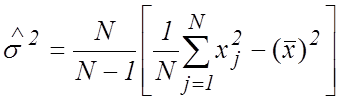 . (11)
. (11)
Полученные оценки (6) и (10) измеряемой величины и дисперсии погрешности являются точечными оценками. Рассмотрим оценивание этих величин с помощью доверительных интервалов.
|
Рис. 2. |
Сформулируем сначала общий
подход к интервальному оцениванию параметров. Предположим, что необходимо
получить доверительный интервал для некоторого параметра ![]() , для которого вычислена точечная
оценка
, для которого вычислена точечная
оценка ![]() и известна плотность распределения
этой оценки
и известна плотность распределения
этой оценки  (рис.2).
(рис.2).
Пусть задана доверительная
вероятность P. Построить доверительный интервал – это значит найти его
границы ![]() и
и ![]() такие,
что:
такие,
что:
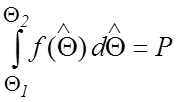 .
.
Чтобы сформулированная задача имела единственное решение, сделаем следующие логически обоснованные допущения:
1)
математическое ожидание ![]() равно вычисленной точечной оценке
равно вычисленной точечной оценке ![]() ;
;
2)
вероятности того, что истинное
значение ![]() оцениваемого параметра лежит выше
верхней границы
оцениваемого параметра лежит выше
верхней границы ![]() или ниже нижней границы
или ниже нижней границы ![]() доверительного интервала, одинаковы
и равны
доверительного интервала, одинаковы
и равны ![]() , т.е. границы
, т.е. границы ![]() и
и ![]() симметричны
относительно
симметричны
относительно ![]() для симметричных относительно
математического ожидания законов распределения
для симметричных относительно
математического ожидания законов распределения ![]() .
.
Определим доверительный
интервал для истинного значения с измеряемой величины. Границы этого интервала
зависят не только от оценки ![]() измеряемой
величины, но и от оценки
измеряемой
величины, но и от оценки ![]() среднего
квадратического отклонения погрешности. Для построения доверительного интервала
необходимо вычислить величину [1-3]
среднего
квадратического отклонения погрешности. Для построения доверительного интервала
необходимо вычислить величину [1-3]
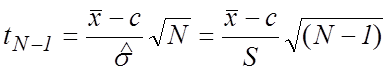 . (12)
. (12)
При нормальном распределении
погрешностей величина ![]() распределена по закону
Стьюдента с
распределена по закону
Стьюдента с ![]() степенями свободы (
степенями свободы (![]() -распределение). Распределение
Стьюдента зависит от числа опытов
-распределение). Распределение
Стьюдента зависит от числа опытов ![]() . В специальных
таблицах [1-3] приведены значения
. В специальных
таблицах [1-3] приведены значения ![]() для величины
для величины ![]() , имеющей распределение Стьюдента с
, имеющей распределение Стьюдента с ![]() степенями свободы, определяемые из условия
степенями свободы, определяемые из условия
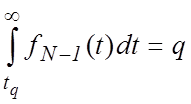 ,
,
где ![]() – плотность
– плотность ![]() -распределения. Полагая
-распределения. Полагая ![]() (
(![]() –
доверительная вероятность) и зная
–
доверительная вероятность) и зная ![]() , по таблице
находим границу
, по таблице
находим границу ![]() .
.
Подставив в (12) значение ![]() вместо
вместо ![]() ,
получим границы доверительного интервала для измеряемой величины:
,
получим границы доверительного интервала для измеряемой величины:
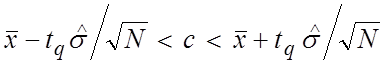 . (13)
. (13)
При построении доверительного
интервала для дисперсии ![]() случайной
погрешности используют случайную величину [1-3]
случайной
погрешности используют случайную величину [1-3]
![]() . (14)
. (14)
которая при нормальном распределении погрешностей распределена по
закону 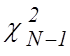 с
с ![]() степенями
свободы. В таблицах [1-3] приведены значения
степенями
свободы. В таблицах [1-3] приведены значения ![]() для
величины
для
величины ![]() , имеющей
, имеющей ![]() -распределение
с
-распределение
с ![]() степенями свободы, определяемые из
условия
степенями свободы, определяемые из
условия
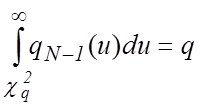 ,
,
где ![]() – плотность
– плотность ![]() -распределения. Так как это
распределение не симметрично, то по таблице необходимо указать значения верхней
и нижней границ интервала
-распределения. Так как это
распределение не симметрично, то по таблице необходимо указать значения верхней
и нижней границ интервала 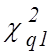 и
и 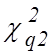 , соответствующие вероятностям
, соответствующие вероятностям ![]() и
и ![]() ,
где
,
где ![]() – доверительная вероятность.
Подставив вместо
– доверительная вероятность.
Подставив вместо ![]() из (14) найденные значения
из (14) найденные значения
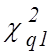 и
и 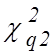 ,
получим границы доверительного интервала для дисперсии:
,
получим границы доверительного интервала для дисперсии:
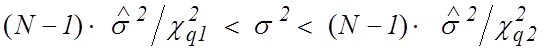 . (15)
. (15)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.