Вероятностное описание погрешностей измерения, страница 18

В такой постановке задача является частным случаем задачи (2) из раздела 1, когда относительно погрешностей  сделаны те же самые допущения. В этом случае оценки коэффициентов  и  получаются из формулы (8):

,                        (16)

,                              (17)

где обозначено

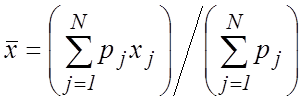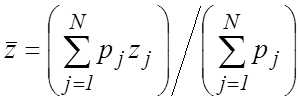,       ,            (17а)

,    .

3.3. Полиномиальная регрессия

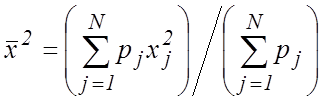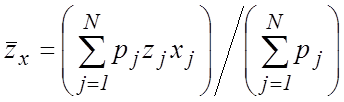Согласно теореме Вейерштрасса [9] любую непрерывную функцию  можно приблизить на конечном интервале сколь угодно точно полиномом -го порядка

,           

выбрав соответствующие степень полинома  и коэффициенты .

Поэтому задача нахождения коэффициентов регрессии  по измеренным значениям  ( – ошибки измерения) функции , выполненных при фиксированных точно известных значениях  независимой переменной , актуальна.

Пусть имеется система из  уравнений относительно  неизвестных :

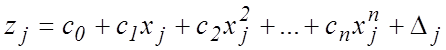,       ,   (18)

причем предполагается, что , а погрешности  удовлетворяют условиям 1) и 2) раздела 1. Требуется найти оценки неизвестных коэффициентов  из системы (18). Т.к. число уравнений больше числа неизвестных, то данную систему надо решать по ММП. В этом случае матрица плана эксперимента имеет вид

.                     

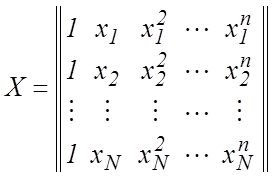Введем обозначения

     ,    

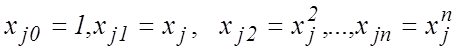
Тогда система (18) примет вид, аналогичный (2)

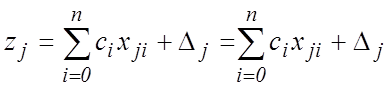
      .   (19)

А оценки неизвестных коэффициентов , параметра  и дисперсионной матрицы ошибок  находятся по формулам (8)-(10).

После нахождения коэффициентов полиномиальной регрессии необходимо проверить гипотезу адекватности представления рассматриваемого явления выбранной моделью. Другими словами, необходимо ответить на вопрос, насколько хорошо описывает выбранный полином  изменение функции  в рассматриваемом диапазоне изменения параметра ; и если точность описания неудовлетворительна, то  следует увеличить степень полинома .

Статистически грамотно решить поставленную задачу можно только в случае, когда известна дисперсия исходных наблюдений  (или ее можно оценить каким-либо другим способом, отличным от (9)).

Пусть имеется исходная оценка параметра , которую обозначим . Тогда для выбора адекватной модели функции  (то есть степени  полинома  и соответствующих коэффициентов регрессии ) в рассматриваемом диапазоне изменения  можно воспользоваться следующей методикой. Предположим, что априорно (до опыта) ориентировочно известна степень полинома , удовлетворительно описывающая поведение функции  в рассматриваемой области (в случае отсутствия априорных данных лучше всего начать процедуру подбора степени полинома с , то есть ). Используя наблюдаемые значения , находят с помощью (8) оценки коэффициентов  и остаточную дисперсию

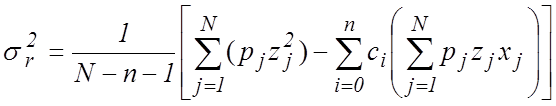.  (20)

Далее составляется -отношение

,                            

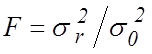и по критерию Фишера проверяют (см. часть II, раздел 3), значимо ли отличаются дисперсии остаточная и исходных наблюдений. Если отличие незначимое, то с заданной доверительной вероятностью считают, что полином  адекватно описывает поведение функции  на заданном интервале. В противном случае увеличивают степень полинома на единицу и повторяют процедуру с полиномом , и т.д. пока отличие не перестанет быть значимым. Следует отметить, что вычисление остаточной дисперсии по формуле (20) проще, чем по формуле (9), т.к. часть входящих в (20) сумм была уже подсчитана при вычислении оценок коэффициентов регрессии.

Важно понимать, что данные методы нахождения коэффициентов  регрессии и проверки гипотезы адекватности модели можно применять и в случае, когда вместо степенных функций   используются любые другие известные функции параметра , например, гармонические,  и т.д.

4. Примеры совместных измерений

4.1. Исследование зависимости сопротивления проводника от температуры

С целью установления зависимости сопротивления медного проводника от температуры  были проведены совместные измерения его температуры  и сопротивления . Данные приведены в таблице 1. Предполагая, что априори известен линейный характер этой зависимости

,                       

где  – сопротивление проводника при температуре ;  – температурный коэффициент сопротивления, необходимо из экспериментальных данных оценить неизвестные коэффициенты  и . Температура .

Используя заданный вид зависимости сопротивления медного проводника от температуры и экспериментальные данные, составим систему из  уравнений

           .   (21)

Преобразуем систему (21) к виду

             .   (22)

Введем обозначения ; ; ; . Тогда система (22) примет вид, полностью совпадающий с (15). Если теперь предположить, что наблюдаемые значения сопротивления известны с погрешностями, которые распределены по нормальному закону с нулевым математическим ожиданием и неизвестной, но одинаковой дисперсией , то систему (22) можно решить по МНК. Оценки коэффициентов  и  будут задаваться выражениями (16) и (17), где все весовые коэффициенты .

1	19.989	20		0
2	20.083	21	1	1
3	20.172	22	2	4
4	20.235	23	3	9
5	20.319	24	4	16
6	20.412	25	5	25
7	20.475	26	6	36
8	20.555	27	7	49
9	20.647	28	8	64
10	20.713	29	9	81
11	20.808	30	10	100
12	20.869	31	11	121
13	20.962	32	12	144
14	21.033	33	13	169
15	21.112	34	14	196
16	21.205	35	15	225
17	21.283	36	16	256
18	21.365	37	17	289
19	21.446	38	18	324
20	21.524	39	19	361
21	21.585	40	20	400