Вероятностное описание погрешностей измерения, страница 3

Широкое распространение этого распределения обусловлено тем, что в соответствии с центральной предельной теоремой сумма большого числа случайных величин сходится к нормальному распределению независимо от вида распределений этих слагаемых. Погрешности измерения, особенно для прецизионных СИ, вызваны совокупным влиянием большого количества факторов, не поддающихся непосредственному учету. Поэтому предположение о нормальном законе распределения случайных погрешностей измерения во многих случаях оказывается справедливым.

Примерный вид нормальных плотностей вероятностей показан на рис.2. Математическое ожидание случайной величины, распределенной по нормальному закону (4.1), равно , а дисперсия .

На рисунке показаны три кривые для .

Функция распределения нормальной случайной величины имеет вид

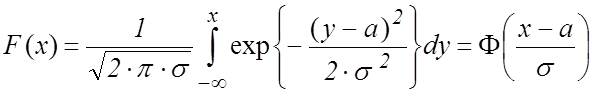,                 (4.2)

где 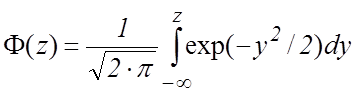 – табулированный интеграл Лапласа.

Распределение хи-квадрат. Такое распределение имеет сумма квадратов независимых случайных величин с нулевым математическим ожиданием и единичной дисперсией. Число слагаемых  называется числом степеней свободы. Это распределение используется при построении доверительных интервалов для оценок дисперсий и имеет вид:

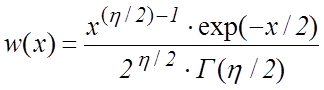,                                   (4.3)

где  – гамма функция Эйлера.

Распределение Стьюдента. Такое распределение имеет случайная величина

,                                                             

где  – распределено нормально с нулевым математическим ожиданием и единичной дисперсией;  – имеет распределение хи-квадрат с  степенями свободы. Оно используется при определении доверительных интервалов результатов прямых измерений при экспериментально оцениваемой дисперсии.

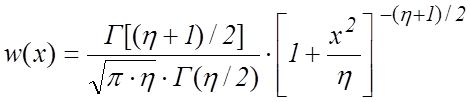.                        (4.3)

Распределение Фишера. Такое распределение имеет величина

,

где величины  имеет распределение хи-квадрат с  степенями свободы . Такое распределение используется при анализе оценок дисперсий случайных величин. Оно табулировано для различных значений , .

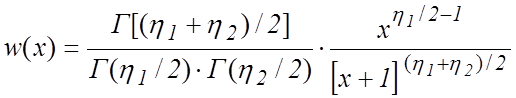.                            (4.4)

5. Системы случайных величин и их характеристики

С системами случайных величин сталкиваются во всех случаях, когда результаты эксперимента характеризуются несколькими случайными величинами, которые в силу взаимной зависимости необходимо рассматривать как единое целое, например, как случайный вектор , где знак  обозначает операцию транспонирования матрицы. С системами случайных величин имеют дело при обработке результатов косвенных, совокупных и совместных измерений.

Способы описания системы случайных величин аналогичны способам описания одномерных случайных величин. Исчерпывающими вероятностными характеристиками системы из  случайных величин является -мерная функция распределения

                              (5.1)

или -мерная плотность вероятности

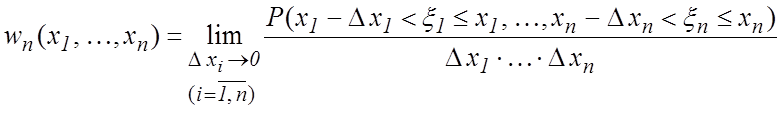.   (5.2)

Как и в случае одномерном, многомерные функции распределения и плотности вероятности взаимнооднозначно определяют друг друга:

,                                

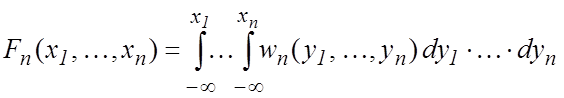.                     (5.3)

Многомерная функция распределения удовлетворяет следующим условиям:

1) ;

2) ;                                                                        ,

3)  ,         .

Свойства многомерной плотности вероятностей аналогичны свойствам одномерной:

1) ;

2) 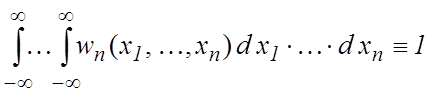.                                                                   (5.4)

Аналогично (2.7) определяется вероятность пребывания случайного вектора  в любой области  -мерного пространства :

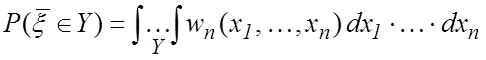.                      (5.5)

Если координаты случайного вектора статистически независимы, то

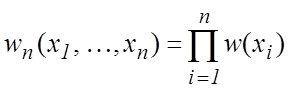.                                        (5.6)

Это соотношение является необходимым и достаточным условием для статистической независимости случайных величин.

Математическим ожиданием функции  нескольких случайных величин называется число

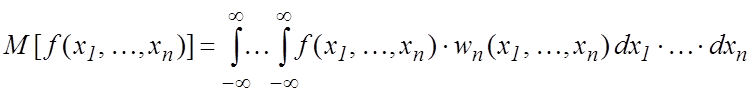.         (5.7)

Для -мерного случайного вектора  также вводятся понятия математических ожиданий его компонент и вторых центральных моментов:

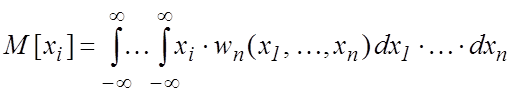,                            (5.8)

,                                

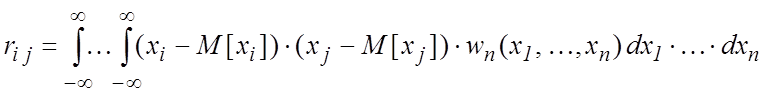.         (5.9)

Очевидно, что . Матрица, компоненты которой являются случайными величинами, называется случайной матрицей. Математическим ожиданием  случайной матрицы  называется матрица, компоненты которой равны математическим ожиданиям компонент матрицы .

Симметрическая матрица , компонентами которой являются величины  из (5.9), называется ковариационной матрицей случайного вектора . В матричном виде выражение для нее будет:

.                        (5.10)

Для независимых случайных величин  справедливы следующие важные свойства:

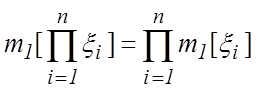,                                  (5.11)

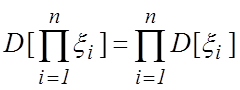.                                     (5.12)

В приложениях метода наименьших квадратов часто приходится иметь дело с -мерным случайным вектором , компоненты которого распределены по нормальному закону и представляют собой случайные погрешности наблюдения. При этом зачастую составляются линейные комбинации наблюдений и их погрешностей вида:

,                                                      (5.13)

где  – случайный вектор, получающийся из вектора  путем линейного преобразования, задаваемого матрицей  размера . Если  и ранг матрицы  равен , то вектор  будет называться невырожденным, и его компоненты тоже будут распределены нормально. Причем вектор математических ожиданий :

,                                         (5.14)

а ковариационная матрица :

.                                          (5.15)

Для двух случайных величин  и , имеющих совместное распределение  мерой их статистической зависимости является коэффициент корреляции:

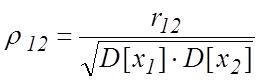,                                            (5.16)

где  – второй центральный момент распределения , задаваемый выражением (5.9). Если , то величины  и  статистически независимы, и наоборот, если 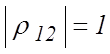, то между  и  существует линейная зависимость.

Введение

Метрология – наука об измерениях, методах и средствах обеспечения их единства, способах достижения требуемой точности.

В метрологии отчетливо отображены два направления.