Рассказать про буквенные обозначения.
(1) - все факторы на нижних уровнях
a,b,c - соответствующий фактор на верхнем уровне, а остальные на нижних.
ab,bc - два указанных фактора на верхних уровнях а остальные на нижних.
Если k фаворов и все на двух уровнях, то ПФЭ с матрицей планирования 2(")
Про активность модели! . Или можно оценить парные (смешанные факторы)
взаимодействия.
![]()
Но оценить ![]() не
удается, т.к. столбец с
не
удается, т.к. столбец с ![]() не будет отличаться от (1). Поэтому оценивается
не будет отличаться от (1). Поэтому оценивается
![]() ,
, ![]() ,
, ![]() ,
, ![]()
См. пункт 8.4.3
Для оценки влияния линейной модели, т.е. (ф-ла стр 89) достаточно КН опыте
а в ПФЭ 2("), т.е. с ростом k возрастает избыточность экспериментов. По этому
ограничиваются дробными репликами. В чем же идея: Имеем модель, т.е.
![]()
достаточно КН опыте в ПФЭ ![]() ,
т.е. с ростом k возрастает избыточность экспериментов. Поэтому часто
организуются дробными репликами. В чем же идея : Имеем модель
,
т.е. с ростом k возрастает избыточность экспериментов. Поэтому часто
организуются дробными репликами. В чем же идея : Имеем модель ![]()
Для этого достаточно 4x опытов: 4 вместо 8. Т.е. можно взять 2k, а не 2k
и вместо парного взаимодействия ![]() .Оценки
.Оценки
![]()
![]()
![]()
(стр 90,91,92 таб и ф-лы)
4.3.3. Понятия о дробной реплике
|
N |
|
|
|
|
Б.О. |
У |
|
1 |
+ |
- |
- |
+ |
|
|
|
2 |
+ |
+ |
- |
- |
a |
|
|
3 |
+ |
- |
+ |
- |
b |
|
|
4 |
+ |
+ |
+ |
+ |
abс |
|
![]()
![]()
1 –ая полуреплика (c,a,b,abc)
![]()
![]()
2 – ая полуреплика (1),ac,bc,ab
![]()
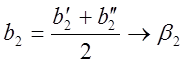
![]()
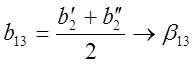
![]()
Как разбивать ![]() на
полуреплики ?
на
полуреплики ?
Понятие генерирующего соотношения
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]()
каждая реплика задается определяющим контрастом – соотношением, задающего элемента первого столбца
![]() ;
; ![]()
Для ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ;
; ![]()
d,ae,be,abd,cde,ac,be,abcde
????(на стр 91)
(##стр 92)
Когда добавляем ![]() ,то
,пологая
,то
,пологая ![]() имеем две полуреплики
имеем две полуреплики
(1), ad, bd, ab, cd, ac, bc, abcd ![]()
d , a , b ,abd, c ,acd, bcd, abc ![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]()
П.Ф.Э. с матрицей ![]()
D.P. П.Ф.Э. с матрицей ![]()
![]()
![]()
Примеры: Uщем модель ![]()
|
N |
|
|
|
y |
|
1 |
+1 |
- |
- |
y1 |
|
2 |
+ |
+ |
- |
y2 |
|
3 |
+ |
- |
+ |
y3 |
![]()
![]()
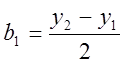
![]()
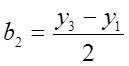
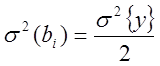
П.Ф.Э. 22 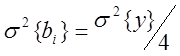
Если теперь k1=8 и k2=31 N1=8 , N2=32
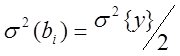 27-4 231-26 N1=8
, N2=32
27-4 231-26 N1=8
, N2=32
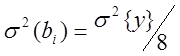
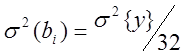
Задача о точном взвешивании.
x1, x2, x3
|
|
x1 |
x2 |
x3 |
y |
|
- |
- |
- |
yo |
|
+ |
- |
- |
y1 |
|
- |
+ |
- |
y2 |
|
- |
- |
+ |
y3 |
|
|
x1 |
x2 |
x3 |
y |
|
- |
- |
+ |
yo |
|
+ |
- |
- |
y1 |
|
- |
+ |
- |
y2 |
|
+ |
+ |
+ |
y3 |
xi=yi-yo ![]()
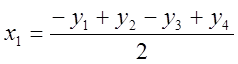
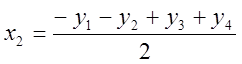
![]()
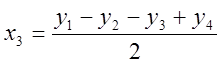
![]()
(##стр 93)
4.2.4 Свойства полного факторного эксперимента.
1) Симметричность относительно центра эксперимента
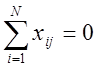 j - номер фактора ; N - число опытов
j - номер фактора ; N - число опытов
2) Условие нормировки
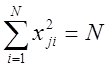
3) Ортогональность матриц плана эксперимента
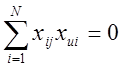
![]()
4) Ротатабельность эксперимента, т.е. точки в матрице планирования подбираются
так, что точность предсказания значений параметра оптимизации одинакова на
равных расстояниях от центра эксперимента и не зависит от направления.
Коэффициенты регрессии находятся из следующих простых выражений:
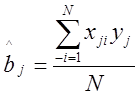
![]()
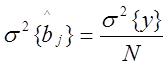
![]()
![]()
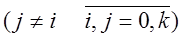
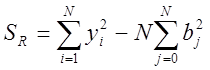 ,
, ![]()
Преимущества
1) Простоты вычисления
2) Все коэффициенты регрессии находятся независимо друг от друга.
3) Все к.р. определяются с одинаковой минимальной дисперсией
4) Рентабельное планирование
1) ![]() -
диагональная
-
диагональная
2) N # ![]() =
= ![]()
1) fR = 0 , SR = 0 насыщенное планирование
2) 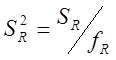
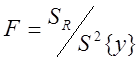 ненасыщенное
планирование
ненасыщенное
планирование
3)Только линейная зависимость и ненасыщенное планирование оценить саму S2{y}
Т.к. все коэффициенты bi находятся независимо друг от друга , то можно проверить их значимость
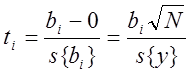
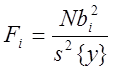 f1=1
, f2 = число степеней свободы
с которыми была определена s2{y}
f1=1
, f2 = число степеней свободы
с которыми была определена s2{y}
Ортогональное планирование
![]()
4.3 Крутое восхождение по поверхности отклика.
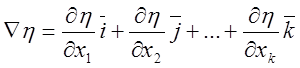
![]()
Теорема Бокса .Оценки коэффициентов ![]()
![]() линейного уравнения регрессии имеют минимальные
дисперсии, если они получены при помощи рентабельного плана первого порядка.
линейного уравнения регрессии имеют минимальные
дисперсии, если они получены при помощи рентабельного плана первого порядка.
Теорема Брукса! Наиболее эффективен поиск коэффициентов, когда N=кн.
4.4 Описание почти стационарной области.
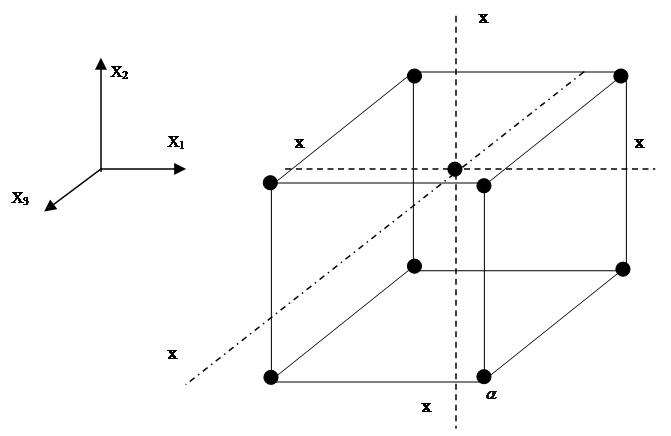 |
1) Дробная ритмика П.Ф.Э. 23-1
2) П.Ф.Э. вершина куба
3) Шесть звездных точек с координатами (см на стр ..)
образуют октаэдр
4) Несколько экспериментов в центре (..)
В общем случае
![]()
8+6+1=15 27 k=3
16+8+1=25 81 k=4
![]()
![]()
 |
Определяющей контраст
![]()
![]()
![]()
![]()
![]()
![]()
6.4.5. Приведение ПЭВ и обработка результатов.
Проводится дублирующие опыты в точках ПФЭ
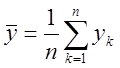
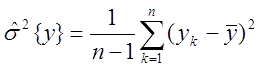
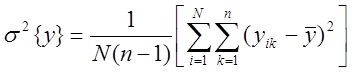
Fотносительное
(## стр 23)
5. Аналоговые измерительные приборы.
Парк их все еще велик. Они достаточно просты. Слабое быстродействие и
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.