Вероятностное описание погрешностей измерения, страница 17

.                           

Тогда

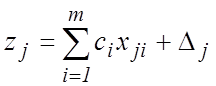,         .    (2)

Относительно погрешностей  сделаем следующие допущения:

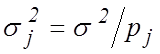1) погрешности  являются нормально распределенными случайными величинами с нулевым математическим ожиданием  и дисперсиями , причем  известны, а параметр  подлежит оцениванию вместе с искомыми параметрами  , то есть измерения  неравноточные;

2) погрешности отдельных измерений независимы. Из (2) следует, что величины  будут иметь нормальное распределение с параметрами

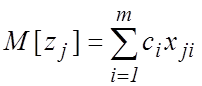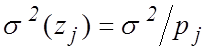,           .          (3)

Естественно, что при решении системы (1) вместо величин  придется использовать наблюдаемые значения , причем число наблюдений, как правило, делают большим числа неизвестных . В этом случае система (2) не имеет решения, поэтому оценки неизвестных параметров получают по методу максимального правдоподобия (ММП) или по методу наименьших квадратов (МНК). С учетом (3) функция правдоподобия выборки  будет

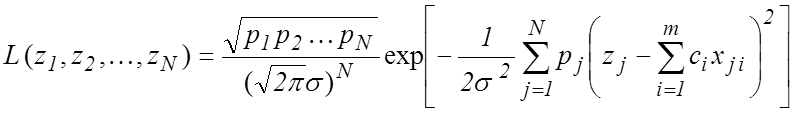.         (4)

Видно, что при всяком значении  максимум функции правдоподобия (4) достигается при выборе  таком, что

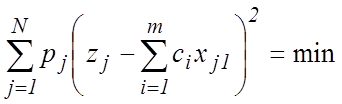,                      (5)

то есть при выборе  по предписанию МНК, который является частным случаем ММП, если выборка  имеет нормальное распределение. Для нахождения минимума (5) найдем  ее частных производных по  и приравняем их нулю. В результате имеем систему из  нормальных уравнений относительно  неизвестных параметров

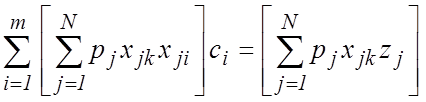
     ,         (6)

решая которую, получают искомые оценки.

Однако более наглядно система (6) и ее решение могут быть представлены в матричном виде. Обозначим ,  – соответственно векторы истинных значений и наблюдаемых значений измеряемых величин;

 ,                     

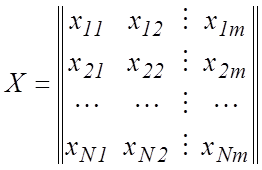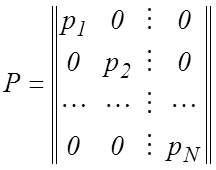
соответственно матрица плана эксперимента, состоящая из известных величин , и диагональная матрица весов измерений;  – вектор неизвестных параметров.

В данных обозначениях система нормальных уравнений (6) примет вид

,                        (7)

а вектор оценок неизвестных параметров находится из выражения

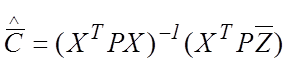,                              (8)

где  и  – обозначают соответственно операции транспонирования и нахождения обратной матрицы. Полученные оценки 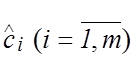являются состоятельными, несмещенными и эффективными [1].

Используя те же экспериментальные данные, можно найти оценку дисперсии случайной погрешности . Для этого продифференцируем логарифм функции правдоподобия (4) по  и приравняем производную нулю, тогда

,                             

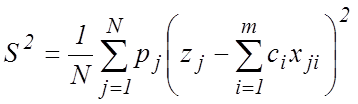где в последнее выражение вместо неизвестных параметров  подставлены их оценки максимального правдоподобия (8). Легко показать, что полученная оценка дисперсии является смещенной [1], а для нахождения несмещенной оценки необходимо ввести поправочный множитель

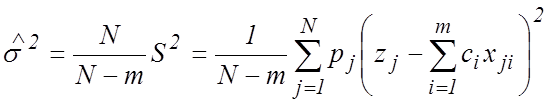.   (9)

Зная оценку параметра , можно судить о точности оценки коэффициентов . Но погрешности оценивания данных коэффициентов уже не независимы, поэтому они описываются дисперсионной матрицей ошибок, равной

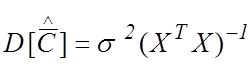.                         (10)

Легко видеть, что 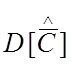 является квадратной, симметричной матрицей ; в диагонали ее стоят дисперсии соответствующих неизвестных параметров , а в недиагональные элементы определяют ковариации соответствующих им параметров .

Основываясь на результатах обработки линейной модели, перейдем к рассмотрению нелинейного случая.

2. Случай нелинейной системы уравнений

Для решения нелинейной задачи осуществляют искусственную линеаризацию системы нелинейных уравнений. Пусть задана система нелинейных уравнений относительно неизвестных параметров , подлежащих оцениванию:

                .  

При этом предполагается, что существует некоторое нулевое приближение  (начальные оценки) неизвестных параметров , причем погрешность его мала, то есть разности  малы по сравнению с истинными значениями оцениваемых коэффициентов  . Не рассматривая способа получения начального приближения , т.к. в каждом конкретном случае это является самостоятельной задачей, остановимся на процедуре уточнения данного приближения. Про погрешности  сделаем те же самые предположения, что и в линейном случае.

Ввиду малости погрешностей разложим функции  в ряд Тейлора в точке , ограничившись линейными членами:

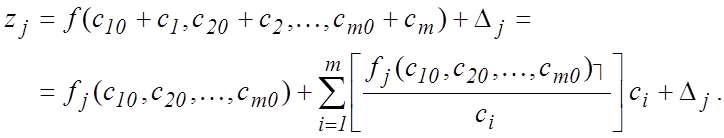          (11)

В системе (11) сначала находятся частные производные  по , а затем вычисляются значения этих частных производных в точке . Получилась система из  линейных относительно поправок  уравнений с  неизвестными, аналогичная системе (2). Решая ее по методике, описанной в предыдущем разделе, находят неизвестные поправки  и вычисляют первые приближения оценок . Данную процедуру можно повторить и найти второе приближение оценок , разложив функции  в ряд Тейлора в точке  и решив получающуюся систему, аналогичную (11), относительно поправок , и т.д. То есть в данном случае оценки неизвестных коэффициентов  находятся методом последовательных приближений. Но для успешной сходимости метода необходимо удачно находить нулевые приближения  , что зачастую является очень сложной задачей.

3. Важные частные случаи

3.1. Случай равноточных измерений

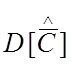Постановка задачи аналогична разделу 1, где погрешности  измерения величин  предполагаются независимыми, нормально распределенными с нулевым математическим ожиданием и одинаковой дисперсией  для всех ; то есть измерения равноточные. В этом случае матрица весов измерений  становится единичной, и выражения для вектора оценок коэффициентов  (8), оценки дисперсии  (9) и матрицы ошибок  (10) несколько упрощаются:

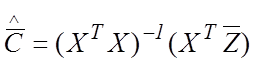,                        (12)

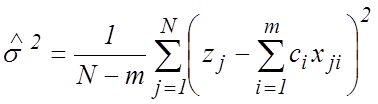,                           (13)

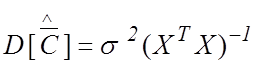.                        (14)

При этом все оптимальные свойства оценок (12) сохраняются.

3.2. Линейная регрессия

Очень часто одна физическая величина  линейно зависит от другой величины  (приведите примеры!)

                             

где неизвестные коэффициенты  и  находят из эксперимента. Для этого при фиксированных точно известных значениях :  измеряют соответствующие значения , но поскольку в измерениях присутствуют неизбежные ошибки , то реально результаты измерения получаются , где измеренные величины  можно представить в виде

.                            (15)