а) В качестве норм указывают пределы допускаемых погрешностей, включающих в себя систематические и случайные составляющие;
б) Порознь нормируются все свойства средств измерений, влияющие на их точность. Основные и дополнительные. Устанавливаются классы точности изделий.
Класс точности – обобщенная характеристика средства измерения, определяемая пределами, допускаемыми основной и дополнительной погрешностями, а также другими свойствами средств измерений, влияющих на точность.
ГОСТ 8.401-80 – способы нормирования метрологических характеристик. Класс точности выражается числом:
![]() ;
; ![]() ;
;![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() (где h=1,
0, -1, -2, и т.д.).
(где h=1,
0, -1, -2, и т.д.).
Правила и примеры обозначения класса точности средств измерения |
||||
Преобладающий вид погрешности |
Форма для определения основной погрешности |
Пределы допуска при погрешности, % |
Обозначение |
Пример |
Аддитивная ИП |
Приведенная
|
|
|
1.5 или 2.5 |
Относительная
|
|
|
2.5 |
|
Аддитивная + мультипликативная ИП |
Относительная
|
|
|
|
|
|
|
Римские цифры и буквы |
||
Аддитивная ИП |
Абсолютные
|
|
||
3. Обработка результатов измерений
3.3. Обработка результатов косвенных измерений
В результате косвенных измерений определяется значение физической величины, функционально связанной с другими физическими величинами, значения которых а1, а2, … , аm.
![]() (3.16)
(3.16)
Пусть каждая величина аj ![]() измерена
с погрешностью
измерена
с погрешностью ![]() . Необходимо оценить
значение погрешности
. Необходимо оценить
значение погрешности ![]() результата
косвенного измерения.
результата
косвенного измерения.
Рассматривая z как функцию m переменных аj , запишем её полный дифференциал:
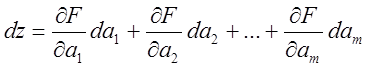 или
или 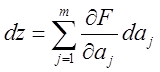 (3.17)
(3.17)
Предположим, что погрешности измерения достаточно малы, заменим в (3.17) дифференциалы соответствующими приращениями:
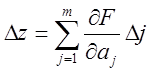 (3.18)
(3.18)
В (3.18) каждое слагаемое вида 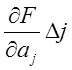 представляет
собой частотную погрешность результата косвенного измерения, вызванную
погрешностью
представляет
собой частотную погрешность результата косвенного измерения, вызванную
погрешностью ![]() измерения величины
измерения величины ![]() . Формула (3.18) – приближенная для
систематической погрешности
. Формула (3.18) – приближенная для
систематической погрешности ![]() .
.
Если 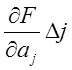 разных знаков, то
происходит частичная компенсация их вклада в
разных знаков, то
происходит частичная компенсация их вклада в ![]() .
.
Если заданы предельные значения погрешностей ![]() , то можно оценить предельную
погрешность
, то можно оценить предельную
погрешность ![]() :
:
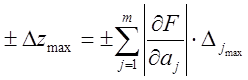 (3.19)
(3.19)
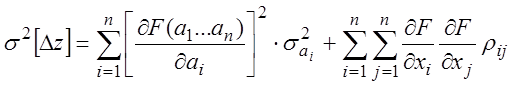
Если же погрешность ![]() независимы,
и математические ожидания их равны 0, то математическое ожидание
независимы,
и математические ожидания их равны 0, то математическое ожидание ![]() будет равно:
будет равно:
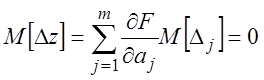 (3.20)
(3.20)
а дисперсия:
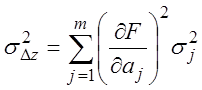 (3.21)
(3.21)
где
![]() - дисперсия погрешностей
- дисперсия погрешностей ![]() .
.
Если проведены серии измерения ![]() -
прямых:
-
прямых:
![]() ,
, ![]() …
…![]() (
(![]() )
)
всего m – серий по kj в каждой. То оценка параметра z будет:
![]() (3.22)
(3.22)
где
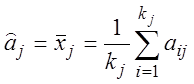 (3.23)
(3.23)
Причем систематическая погрешность ![]() , определяется (3.18), математическое
ожидание случайной погрешности
, определяется (3.18), математическое
ожидание случайной погрешности ![]() равно нулю, а
дисперсия определяется по (3.21).
равно нулю, а
дисперсия определяется по (3.21).
Важные частные случаи.
1. Функция ![]() линейная, т.е.
линейная, т.е. 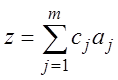 , где сj – известные
коэффициенты. Тогда все:
, где сj – известные
коэффициенты. Тогда все:
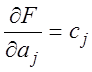
и формулы приобретают вид:
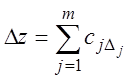
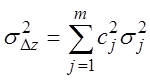
2. Функция ![]() логарифмируема:
логарифмируема:
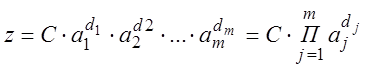
![]() - действительные числа.
- действительные числа.
Прологарифмируем z, а затем
возьмем частные производные по ![]() :
:
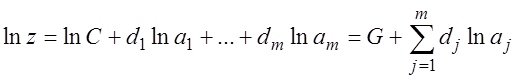
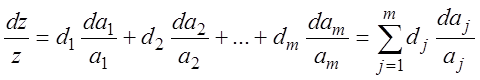
Здесь удобно рассматривать не абсолютную, а относительную погрешность z:
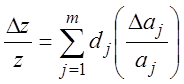
Пример.
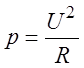 . Пусть
. Пусть ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; 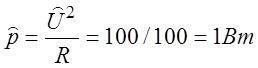 ;
;
![]() .
.
3.6. Погрешности косвенных измерений
Анализ погрешностей косвенных измерений в большинстве случаев заключается в расчете числовых характеристик погрешности определения измеряемой величины по заданным характеристикам погрешностей измерений аргументов.
Если известны истинные значения аргументов ![]() , то истинное значение величины,
измеряемой косвенным методом, будет:
, то истинное значение величины,
измеряемой косвенным методом, будет:
![]() (3.34)
(3.34)
но результаты прямых измерений известны с погрешностями:
![]()
значит
![]()
если
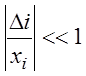 (погрешности
малы),
(погрешности
малы),
то разложим (3.35) в ряд Тейлора:
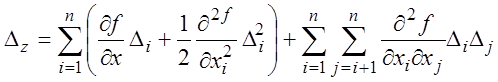 (3.36)
(3.36)
систематическая погрешность:
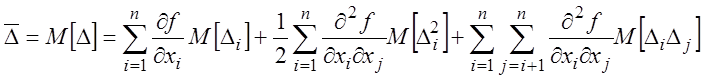
т.к.
![]() - систематическая плюс случайная
составляющие,
- систематическая плюс случайная
составляющие, ![]()
то
![]() ;
; ![]() ;
; ![]() ;
;
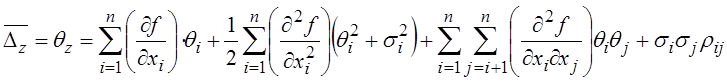 (3.37)
(3.37)
В линейном случае, когда ![]() -
линейная функция:
-
линейная функция:
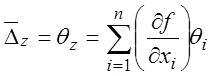 (3.38)
(3.38)
Нелинейная поправка:
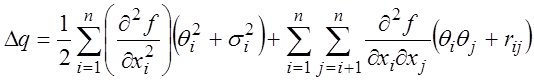 (3.39)
(3.39)
зависит
не только от систематических погрешностей аргументов, но и их случайных
погрешностей. В случае малых погрешностей измерений ![]() поправку
можно не учитывать.
поправку
можно не учитывать.
Для оценки случайной погрешностей измерений необходимо вычесть (3.37) из (3.36) и пренебречь членами, содержащими квадраты погрешностей:
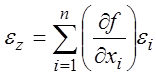
Возводим это равенство в квадрат, и находя математическое ожидание от его обеих частей, имеем:
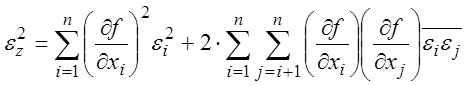
Тогда:
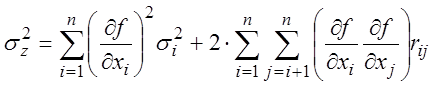 (3.40)
(3.40)
Для независимых погрешностей ![]() :
:
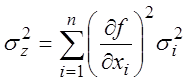 (3.41)
(3.41)
Частные случаи:
![]()
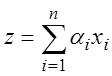 ,
=>
,
=> 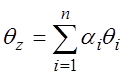
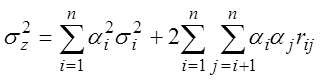
![]()
![]() ;
;
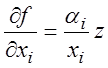
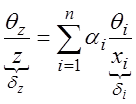 - относительные систематические
погрешности;
- относительные систематические
погрешности;
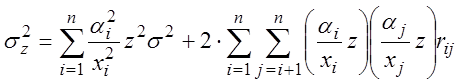
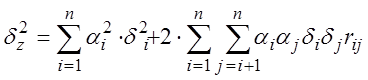
Пример
1. По
результатам прямых измерений емкости ![]() и
и ![]() определена емкость
определена емкость ![]() . Найти погрешности её измерения,
если заданы
. Найти погрешности её измерения,
если заданы ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() . Согласно (3.38) и (3.41)
систематическая и случайная погрешности будут:
. Согласно (3.38) и (3.41)
систематическая и случайная погрешности будут:
![]()
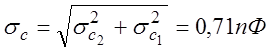
Вводится поправка, для направления результата:
![]()
Для доверительной вероятности ![]() ,
, ![]() :
:
![]() ,
=>
,
=> ![]()
СКО:
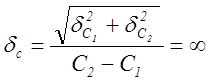 , при
, при ![]() .
.
В нашем примере ![]() , ç
, ç![]() !
!
Рассмотрите случай, когда r12=1?
Пример
2. По
результатам измерения напряжения ![]() и сопротивление
и сопротивление ![]() косвенным методом измерена мощность
косвенным методом измерена мощность 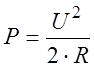 . Определить погрешности её
измерения, если
. Определить погрешности её
измерения, если ![]() ,
, ![]() .
.
По формулам для произведения:
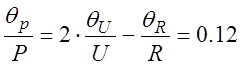
Относительно СКО:
![]()
Мощность ![]() ;
; ![]()
![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]()
Результат измерений:
![]()
В измерительной технике имеют дело с большим количеством массовых явлений. Сюда относится множество измерений, проводимых с помощью одного и того же средства измерений (СИ), характеристики множества СИ одинакового типа и т.д. При этом мы встречаемся как со случайными событиями (отказы СИ, правильные и неправильные решения при контроле, наличие грубых промахов), так и со случайными величинами (погрешности измерения, время безотказной работы, значение контролируемого параметра) и случайными процессами (флуктуации питающих напряжений, тепловые и дробовые шумы электронных устройств). В силу этого аппарат теории вероятностей оказывается наиболее адекватным сути многих задач измерительной техники.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.