Вероятностное описание погрешностей измерения, страница 22

    -1 -предмета нет на весах

    +1 - предмет на весах

Холостое взвешивание нужно для определения смещения нуля. Затем по очереди

взвешивается каждый из предметов:

    А=y₁-y₀; B=y₂-y₀; C=y₃-y₀;

Если предположить, что случайные погрешности отдельных измерений независимы

и имеют дисперсию,  то:

Теперь проведем тот же эксперимент по схеме:

N	a	b	C	Y
1	+1	-1	-1
2	-1	+1	-1
3	-1	-1	+1
4	+1	+1	+1

Здесь вместо холостого взвешивания взвешиваются все предметы вместе.

Тогда массы грузов можно вычислить по формулам

 ;  ;

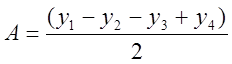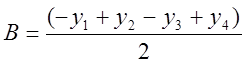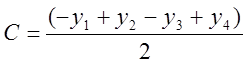
Найдем дисперсию ошибок взвешивания:

Аналогично находим

При такой схеме взвешивания результатов получается вдвое меньше, чем при

традиционном методе, хотя в обоих вариантах нужно провести четыре опыта.

Так как во втором варианте смещение нуля тоже компенсируется то второй план

эксперимента лучше первого, если в качестве критерия сравнения использовать

дисперсию ошибок измерения массы. При первом способе взвешивания, чтобы

получить результаты с такой же точностью, что и во втором, необходимо повторить

дважды все опыты или взять более точный массоизмерительный прибор. По этому в

качестве критериев сравнения используется обычно либо продолжительность,

либо стоимость эксперимента, либо погрешность.

????????#####??????????

##(стр.84)

    Эксперимент, который ставится для решения задач оптимизации называется

экспериментальным .

    Здесь видна глубокая аналогия между оптимизацией и поиском экстремума

некоторой функции.

    Теперь рассмотрим вопрос об объекте исследования. Для описания объекта

исследования его удобно представлять в виде "черного ящика"

(рис...)

 

Стрелки справа изображают численные характеристики целей исследования, или параметры оптимизации , ... , (Целевые функции, выходы и т.д.).

Все способы воздействия на черный ящик , ... , называются факторами

(входы ЧЯ).

    При решении задачи используется математические модели объекта исследования.

Под математической моделью понимается уравнение связывающий параметр оптимизации с факторами:

 У - функция отклика,

##(стр 85)

объекта исследования. При активном эксперименте осуществляется искусственное

воздействие на объект по заранее спланированной программе. Активный эксперимент

лучше, но его труднее осуществить.

 

                                            -управляемые входные параметры (j =1,k )

                                                             -выходные параметры ( i = 1, r  )

                                              -возмущающие воздействия  (l= 1,r )

                                         

                                           

- вычисляемые параметры, характеризующие состоянию объекта. - можно изменить с целью управления входными параметрами. Пусть r = 1, т.е. есть одна выходная переменная. - не контролируемые параметры - случайные величины.

    Основной задачей эксперимента является выявление взаимодействий между

входными и выходными параметрами объекта  и представление их в количественной форме в виде математической модели. Такая модель является математическим отображением наиболее существенных взаимосвязей между параметрами объекта.

##(стр 85а)

4.1.1 Параметры оптимизации.

При планировании экстремального эксперимента очень важно очень важно определить параметр , который нужно оптимизировать . Характеристику цели исследования, заданную количественно, будем называть параметром оптимизации.

Параметр оптимизации - признак, по которому будем оптимизировать процесс. Он должен быть количественным, т.е. задаваться числом. Его необходимо уметь измерять при любых возможных комбинациях выбранных факторов. Множество значений, которые может принимать параметр оптимизации, называется областью его определения. Параметр оптимизации доложен выражаться одним числом. Заданному по выбору значений факторов должно соответствовать одно с точностью до ошибки эксперимента значение параметра оптимизации.(однозначность в статистическом смысле).

Для успешного достижения цели исследования необходимо, чтобы параметр оптимизации действительно оценивал эффективность функционирования системы в заранее выбранном смысле. Это главное требование, определяющее корректность постановки задачи. Необходимо помнить, что речь ведется об эффективности функционирования системы в целом. Если всю систему разбить на несколько подсистем, каждая из которых оценивается своим локальным параметром оптимизации, то оптимальность каждой из подсистем по своему параметру оптимизации не оптимальности всей системы в целом.

Следующее требование к параметру оптимизации требование универсальности и полноты, т.е. всесторонне характеризующие объект. Желательно чтобы п.о. имел физический смысл, был простым и легко вычисляемым.

    При планировании эксперимента с целью нахождения оптимальных условий в качестве единой выходной величены рассматривается критерий оптимальности (целевая функция), зависящий от входных параметров объекта. Эту функцию рассматривают как отклик объекта на указанную комбинацию факторов и называют функцией отклика.

##(стр. 85б)

4.1.2. Факторы.

После выбора параметра оптимизации нужно включить в рассмотрение все существенные факторы, которые могут влиять на процесс. Не учесть какого либо существенного фактора в лучшем случае приведет в росту ошибок измерения.

Фактором называется измеряемая переменная величена, принимающая в некоторый момент времени определенное значение. Факторы соответствуют способам воздействия на объект исследования. Другими словами входные параметры, которые оказывают влияние на объект и могут быть измерены, называются факторы.