Вероятностное описание погрешностей измерения, страница 21

Далее необходимо проверить гипотезу адекватности данной модели. Для этого требуется рассчитать оценку дисперсии  двумя независимыми способами.

Сначала вычисляется оценка остаточной дисперсии по формуле (20) или (13) 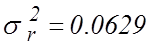. После этого необходимо найти оценку выборочной дисперсии исходных наблюдений , приведенных в таблице 2. Она получается из соотношения

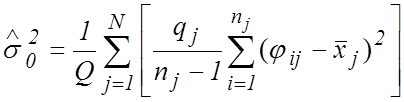,             (27)

где   – веса оценок выборочных дисперсий в сериях наблюдений, пропорциональные числу наблюдений в соответствующей серии, уменьшенному на единицу [10], ;

.                     

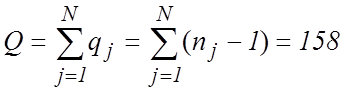Поэтому формулу (27) можно немного упростить для данного частного случая (объясните почему!)

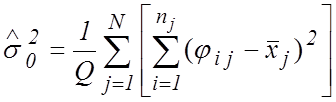.                       (28)

Подставляя в (27) значения из таблиц, имеем .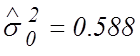

Составляем -отношение 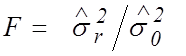, но необходимо учесть, что при вычислении весов  для удобства их всех уменьшили в десять раз, поэтому величину  надо умножить на 10.

.                       

По таблице распределения Фишера для уровня значимости  и чисел степеней свободы  и  находим . Т.к. , то с доверительной вероятностью  (уровнем значимости ) можно утверждать, что полученная модель второго порядка адекватно описывает зависимость поверхностного натяжения от потенциала ртутного электрода в растворе .

Представляет интерес ответ на вопрос, нельзя ли обойтись более простой линейной моделью для описания рассматриваемого явления.

.                         

Оценки коэффициентов  и  рассчитываются по формулам (16), (17) и (17a) с использованием данных из таблицы 3.

;          ;       

;       .    

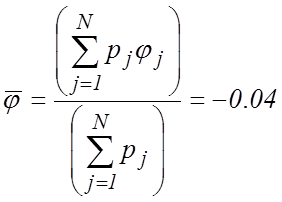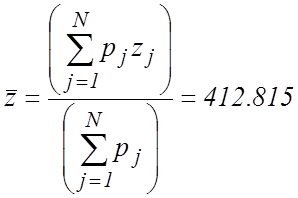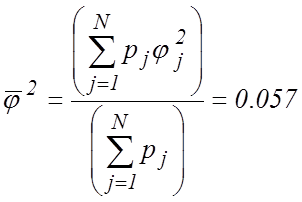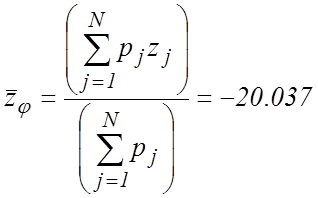Тогда

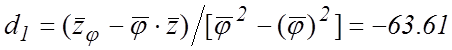,      (16а)

,                      (17а)

и линейная регрессионная зависимость принимает вид

.                        

Теперь проверим гипотезу адекватности полученной линейной модели. Рассчитываем оценку остаточной дисперсии по формулам (13) или (20) 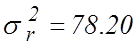. Оценка  уже найдена ранее. Составляем -отношение с учетом того, что его тоже надо умножить на 10.

.                             

По таблице распределения Фишера для уровня значимости  и чисел степеней свободы  и  находим . Т.к. , то с доверительной вероятностью  (уровнем значимости ) можно утверждать, что полученная модель первого порядка неадекватно описывает зависимость поверхностного натяжения от потенциала ртутного электрода в растворе . Поэтому следует пользоваться найденной моделью второго порядка.

Раздел 4

Вопросы планирования эксперимента.

Мысль о том, что эксперимент можно спланировать ,восходит к глубокой древности. Наш далекий предок, убедившейся, что острым камнем можно убить даже мамонта, несомненно выдвигал гипотезы, которые после целенаправленной экспериментальной проверки привели к созданию копья, дротика, а за тем лука со стрелами. Он, однако, не пользовался статистическими методами, поэтому остается непонятным, как он вообще выжил и обеспечил тем самым наше существование.

Статистические методы стали развиваться только в начале нашего века.

открытие идеи планирования эксперимента принадлежит английскому статистику Р. Фишеру (в конце 20-х годов). Планирование экспериментальных экспериментов началось еще через три десятка лет. Первая работа была опубликована в 1951 г. Боксом и Уилсоном. Идея метода Бокса и Уилсона крайне проста. Экспериментатору предлагается ставить отдельные небольшие серии опытов, в каждой из которых одновременно варьируется по определенным правилам все факторы (исследуемые параметры). Серии организуются таким образом, чтобы после математической обработки предыдущей можно было выбрать условия проведения (т.е спланировать) следующую серию. Так последовательно шаг за шагом достигается область оптимума.

В нашей стране ПЭ развивается чуть более четверти века. Интерес вполне понятен: перспектива сократить число опытов, найти оптимум, получить количественные оценки влияния факторов и определить ошибки крайне привлекательна. Но применять методы планирования необходимо очень аккуратно. Если неверно применять методы планирования или выбрать не самый оптимальный путь исследования для данной ситуации, то можно резко снизить эффективность данных методов и даже дискредитировать само направление.

4.1 Основные определения

Эксперимент занимает центральное место в науке. Однако возникает вопрос на

сколько эффективно он используется. Джон Бернал считал что к.п.д. экспериментальной работы примерно 2% математическая теория планирования эксперимента - это один из возможных путей устранения данного недостатка экспериментальных исследований.

........######......???????

Планирование эксперимента - это процедура выбора числа и условия проведения опытов ну и далее для решения задачи с требуемой точностью.

Что здесь существенно стремление к минимизации числа опытов;

 одновременное варьирование всеми переменными, определяющими процесс, по специальным правилам; - алгоритмам; - использование математического аппарата, формализующего многие действия   экспериментатора;

- выбор четкой стратегии, позволяющей принимать обоснованные решения после

  каждой серии экспериментов.

Планирование эксперимента позволяет значительно интенсифицировать труд

исследователя. Сократить сроки и затраты на эксперимент, повысить достоверность выводов по результатам исследований. Целью планирования эксперимента

является выбор множества возможных планов проведения эксперимента одного, в некотором смысле наилучшего. Необходимость сравнения различных планов требует использования критерия сравнения или целевой функции, которые дали бы основание утверждать, что один эксперимент или план эксперимента лучше или хуже другого.  

Где может использоваться планирование эксперимента?

????? Пример хорошего или плохого эксперимента.

Пусть необходимо определить массы трех предметов А,В,С с помощью некоторого

массоизмерительного устройства. Традиционный способ.

N	a	b	C	Y
1	-1	-1	-1
2	+1	-1	-1
3	-1	+1	-1
4	-1	-1	+1