Вероятностное описание погрешностей измерения, страница 10

Любая функция  от величин x_i  называется статистикой. В общем случае она может быть дискретной или непрерывной, но в дальнейшем будут рассматриваться только непрерывные статистики.

Примеры статистик:

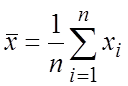              – выборочное среднее,

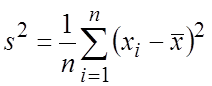  – выборочная дисперсия,

                        – наибольший элемент выборки.

1.2. Оценивание параметров

Допустим, что имеется выборка из n случайных величин, которые полностью характеризуются их совместной плотностью вероятностей

          ,  (1.1)

зависящей от m параметров . В математической статистике плотность вероятностей называется функцией правдоподобия выборки.

В случае повторной выборки:

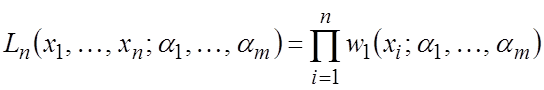               (1.2)

Задача заключается в нахождении значений  неизвестных параметров распределения по полученным значениям . Естественно, что на основании конечной выборки нельзя получить точные значения искомых параметров, так как выборка случайная. Можно сделать лишь некоторые оценки данных параметров или, другими словами,  оценить их значения.

Для этого формируются m статистик:

         

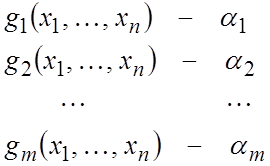
т.е. строятся m функций , которые необходимо выбрать так, чтобы они давали в некотором смысле "хорошее" приближение к соответствующим величинам . Тогда статистики  называются оценками параметров .

Пример. Имеется выборка  из генеральной совокупности нормально распределенных величин с заданными математическим ожиданием a и дисперсией s². Символически это записывается так:

          .

Допустим, что величины x_i независимы, тогда выборка – повторная, поэтому

.

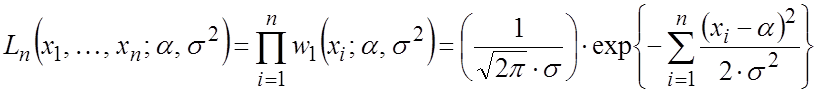Видно, функция правдоподобия выборки зависит от двух параметров a и s², которые необходимо оценить по имеющимся наблюдениям . Т.е. надо построить такие функции  и , которые давали бы хорошее приближение к параметрам a и s².

1.3. Несмещенные и состоятельные оценки.

В общем случае вектор оценок  называется вектором несмещенных оценок параметров , если

          ,      (1.3)

где M[…] – математическое ожидание случайной величины.

Почему необходимо стремиться получать несмещенные оценки параметров a_i? Приведем простой пример. Известно, что

  ,

т.е. в 95 % случаев оценка g_i будет заключена в данных пределах. Допустим теперь, что измерения проведены очень точно, разброс ошибок очень маленький, и . Тогда все реализации оценки  будут группироваться вокруг величины M[g_i] в очень узком интервале. И если теперь , то, несмотря на очень точные измерения с маленьким разбросом, оценка параметра a_i будет найдена с ошибкой. Таким образом, одним из критериев качества оценки является ее несмещенность.

Часто, однако, приходится искать не несмещенные, а асимптотически несмещенные оценки, т.е. такие, которые становятся несмещенными при  (при увеличении объема выборки).

Оценка g_i некоторого параметра a_i называется состоятельной, если для любого e:

           при .

Другими словами, оценка сходится по вероятности к своему истинному значению при увеличении объема выборки.

Состоятельность оценки является вторым критерием ее качества. Потому что, если оценки получаются несостоятельными, то для их получения не имеет смысла проводить большое число наблюдений, так как это не ведет к повышению точности оценивания.

Пример. Статистика  – выборочное среднее является несмещенной оценкой параметра a нормального распределения, а оценка выборочная дисперсия s² (см. предыдущие примеры) является ассимптотически несмещенной оценкой параметра s² того же распределения. В математической статистике доказано, что

           и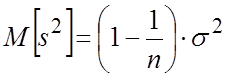 

т.е. s² занижена в меньшую сторону. Очевидно, что несмещенной оценкой параметра s² будет

          ,

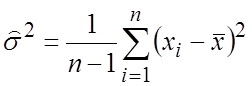но и статистика s² будет практически несмещенной при большом n.

1.4. Точность оценивания параметров

Допустим теперь, что при оценивании параметров научились строить такие функции , которые дают несмещенные и состоятельные оценки параметров . В этом случае за характеристику точности оценок естественно выбрать их дисперсию , т.е. меру разброса вокруг значения . В математической статистике показано, что лучше всего за меру точности несмещенных оценок выбрать вес оценки, т.е. величину:

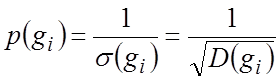          .          (1.5)

Встает вопрос, как точно можно оценивать параметры a_i при заданном объеме выборки n. Другими словами, как сильно можно уменьшить дисперсию (увеличить вес) оценки при заданном n? Ответ на этот вопрос дали Крамер и Рао независимо друг от друга.

Сначала рассмотрим случай оценивания одного параметра. Пусть функция правдоподобия выборки зависит от одного параметра, так что она имеет вид , и пусть имеется статистика  несмещенная оценка параметра a. Крамер и Рао показали, что в этом случае:

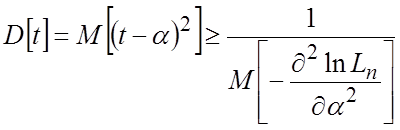          ,    (1.6)

где:

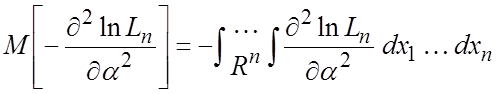          .          (1.7)

Величина (1.7) при условии сходимости интеграла называется информационным количеством Фишера. Эта величина не зависит от способа оценивания a, т.е. от статистики  и представляет собой нижнюю границу точности любой оценки. Другими словами, при заданном объеме выборки точность несмещенной оценки параметра aбудет ограничена снизу.

В случае повторной выборк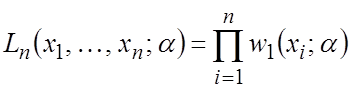и:

           и ,

Тогда из (1.6), (1.7) легко подсчитать:

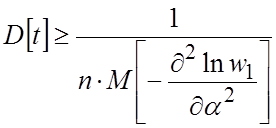          , (1.8)

а вес оценки

          .

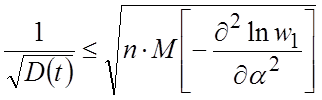В весьма широком классе несмещенных оценок вес оценки при повторной выборке не может быть больше величины, пропорциональной квадратному корню из числа наблюдений. Оценка t_e, для которой в неравенствах (1.6), (1.8) достигается знак равенства, называется эффективной.

Пример. Возвращаясь к примеру оценки параметра a нормального распределения, получаем:

          .

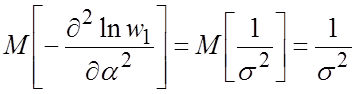Откуда

          .          (1.9)

Для выборочного среднего  получается:

          .          (1.10)

Т.е. оценка  имеет максимально возможную точность и является эффективной.

В случае оценивания нескольких параметров  функция правдоподобия имеет вид (1.1). Пусть статистики

          (1.11)

являются несмещенными оценками соответствующих параметров.

Составим матрицу

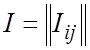          , где 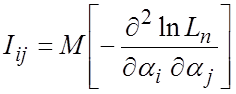.      (1.12)

Матрица I называется информационной матрицей Фишера. А квадратичная форма  является положительно полуопределенной. Будем считать, что , где . Тогда