Вероятностное описание погрешностей измерения, страница 8

В зависимости от множества возможных значений случайной величины различают дискретные и непрерывные случайные величины. Если случайная величина может принимать конечное (или счетное) множество значений, то она называется дискретной. Если случайная величина может принимать любое значение из некоторого интервала или совокупности интервалов, то она называется непрерывной.

Дискретные случайные величины полностью характеризуются вероятностями своих отдельных значений:

,    .

Для счетного множества . При этом равенство  является случайным событием.

Поскольку равенства  образуют полную группу событий, то по формуле (1.9) получаем:

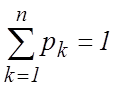.                        (2.1)

Исчерпывающим вероятностным описанием непрерывной случайной величины является задание законов распределения: функции распределения или плотности вероятности.

Функция распределения  определяется следующим образом:

.                        (2.2)

Текущий аргумент  пробегает в общем случае все значения от  до . Можно задать любое конкретное  и по функции распределения определить вероятность того, что произойдет случайное событие , наступление или «ненаступление» которого зависит от заранее неизвестного значения случайной величины.

Из определения  вытекают ее свойства:

1)  ( – невозможное событие);

2)  ( – достоверное событие);

3) ,  – неубывающая функция своего аргумента.

Зная функцию распределения, можно рассчитать вероятность пребывания  в интервале . Случайное событие  можно представить в виде суммы несовместных событий  и . В соответствии с выражением (1.8) и учетом определения (2.2):

.                             

Откуда

.                              (2.3)

Плотность вероятности  определяется следующим образом:

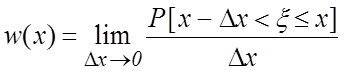.                      (2.4)

Непосредственно из определений (2.2), (2.4) следует:

;                     

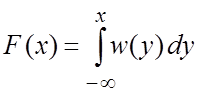.                      (2.5)

В прикладных задачах основное применение находит плотность вероятностей. Учитывая (2.5) и свойства функции , можно получить следующие свойства функции :

1) ;

2) условие нормировки плотности вероятности:

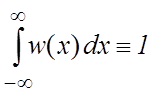.                             (2.6)

С учетом (2.3), (2.4) плотность вероятности можно выразить через вероятность пребывания  в интервале :

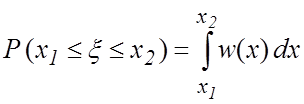.                            (2.7)

Использование термина "плотность вероятности" связано с тем, что по аналогии с традиционным определением плотности (например, отношением массы к объему, который она занимает) значение плотности вероятности представляет собой отношение вероятности попадания в заданный интервал  к величине этого интервала. Поэтому результаты многократных экспериментов гуще, плотнее расположены в окрестности тех точек , которым соответствует большее значение плотности , и менее плотно в тех точках, где  меньше.

В случае дискретной случайной величины  выражение для плотности вероятности принимает вид

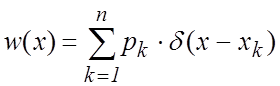,                               (2.8)

где  – дельта-функция Дирака, определяемая следующими соотношениями и свойствами

;    ;   ,

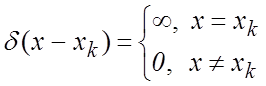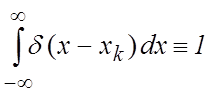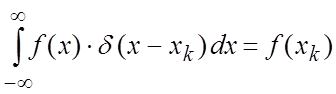 – произвольная функция.

Функция распределения, соответствующая плотности вероятностей (2.8), будет иметь ступенчатый вид, а на рис. 1 показаны характерные графики функций  и  в непрерывном случае.

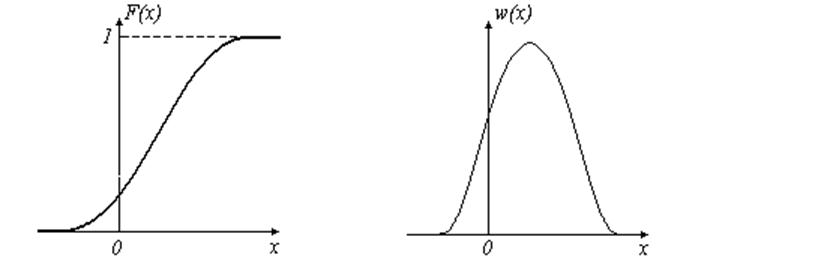
Рис. 1.

3. Числовые характеристики случайных величин

Законы распределения дают исчерпывающее вероятностное описание любой случайной величины. Однако не всегда удается их получить. Кроме того, в некоторых задачах, в частности при нормировании погрешностей, желательно иметь более компактное описание, ограничивающееся заданием одной или нескольких числовых величин. Такими величинами являются моменты распределений (начальные и центральные).

Начальным моментом k-го порядка называется число

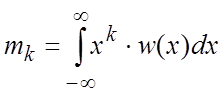.                             (3.1)

Центральным моментом k-го порядка называется число

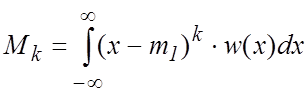,                           (3.2)

где  – начальный момент первого порядка.

Наиболее часто используемые числовые характеристики распределений случайных величин – математическое ожидание и дисперсия.

Математическим ожиданием случайной величины называется начальный момент первого порядка:

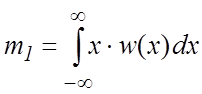.                      (3.3)

Такое определение применимо как для непрерывных, так и для дискретных случайных величин. В последнем случае  задается соотношением:

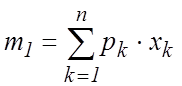.                        (3.4)

Дисперсией случайной величины называется центральный момент второго порядка:

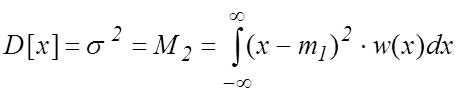,      (3.5)

где  – математическое ожидание, определяемое из (3.3), а  – среднеквадратическое отклонение случайной величины (СКО).

Для дискретной случайной величины

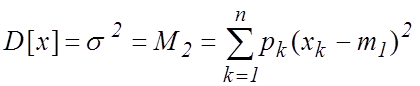,           (3.6)

а  вычисляется из (3.4).

Из (3.5), (3.6) видно, что дисперсия не может быть отрицательной. Она может служить мерой разброса случайной величины относительно математического ожидания. Действительно, если  детерминирована и равна , то есть, разброса нет. Тогда  и , а дисперсия из (3.6) равна нулю. Если же  случайна, и разброс есть, то .

С помощью неравенства Чебышева можно оценить вероятность больших отклонений случайной величины от ее математического ожидания, если известна дисперсия. Для любых

.                              (3.7)

Известны следующие свойства математического ожидания и дисперсии случайной величины.

,          (3.8)

,                              (3.9)

,                          (3.10)

где  – математическое ожидание случайной величины , ,  – некоторые константы.

4. Распределения, часто встречающиеся в задачах метрологии

Нормальное распределение. Одним из наиболее часто используемых распределений является нормальное распределение:

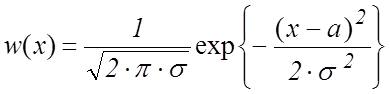.               (4.1)

Широкое распространение этого распределения обусловлено тем, что в соответствии с центральной предельной теоремой сумма большого числа случайных величин сходится к нормальному распределению независимо от вида распределений этих слагаемых. Погрешности измерения, особенно для прецизионных СИ, вызваны совокупным влиянием большого количества факторов, не поддающихся непосредственному учету. Поэтому предположение о нормальном законе распределения случайных погрешностей измерения во многих случаях оказывается справедливым.