Вероятностное описание погрешностей измерения, страница 23

Под областью определения фактора понимается совокупность всех значений, которые в принципе может принимать фактор. Считается что фактор создан, если вместе с его названием указана область его определения. Она может быть непрерывной или дискретной. В задачах планирования, которые мы будем рассматривать, всегда будем использовать дискретные области определения. Т.е. даже для факторов с непрерывной областью определения (температура, давление, количество вещества) мы будем предполагать, что выбегаются дискретные множества их значений, называемые множествами уровней фактора. Если фактор принимает экспериментах несколько значений, то такие значения называются уровнями. В каждом отдельном эксперименте фактор находится на определенном уровне. Максимально возможное значение фактора - верхний уровень, минимально возможное нижний уровень. Зафиксировав набор уровней для каждого фактора в эксперименте мы полностью задали все возможные состояния черного ящика и задали число возможных опытов эксперимента.

##(стр 85в)

Факторы делятся на количественные и качественные ( t ,T,C, скорость передачи вещества) и (размытые реагенты, абсорбенты, кислоты, металлы) Хотя качественным факторам не соответствует числовая шкала в том смысле, в каком она понимается для количественных факторов, однако для них можно построить условную порядковую шкалу, которая ставит  в соответствие уравнением качественного фактора числа натурального ряда, т.е. проводит кодирование. Порядок уравнений может быть произвольным но он после кодирования фиксируется.

Требования к факторам. Факторы должны быть управляемыми, т.е. факторы можно поддерживать на заданных уровнях. Должна быть указана последовательность действий (операций), помощью которых устанавливается заданное значение фактора в опыте (уровень).Точность замера факторов должна быть возможно более высокой. Однозначность фактора, т.е. он не должен завесить от других факторов.

Изучим процесс растворения твердого тела в жидкости - диффузионный процесс. Может ли скорость диффузии служить фактором в планировании эксперимента?

По этому ответ на этот вопрос отрицательный. Совместимость факторов. Независимость факторов "Примеры так же получены, как и правила" (Ньютон)

4.1.3 Выбор модели

Под моделью понимается вид функции отклика

y =   (6.1)

Выбрать М - выбрать уравнение этой функции.

##(стр 85г)

После этого необходимо будет спланировать эксперимент для оценки численных коэффициентов этого уравнения. Но как выбрать модель?

Уравнение (6.1) задает в n+1-мерном пространстве гиперповерхность. Для наглядности будем считать n=2, тогда в трехмерном пространстве можно изобразить эту поверхность

 

                                                                                     y

 

       max

    

        min                                                                                                                    

 

                       max      min       

                                                                         

Внутри прямоугольника лежат все всевозможные состояния "черного ящика". Все n+1-мерное пространство - факторное пространство.

Один из возможных путей планирования - полный перебор, но он в реальных задачах редко приводит к успеху.

Другая возможность - случайный поиск.

Третья возможность - построение математической модели, чтобы с ее помощью предсказать значение Ф.О. в тех точках, которые не изучались экспериментально.

За отказ от полного перебора надо чем-то платить. Цена - это предположение, сделанные априори о свойствах нашей модели. Некоторые из предположений мы не можем проверить на опыте. Они называются постулатами. И если исходные постулаты не выполняются, то можно ни когда не найти оптимума y, вернее за оптимум мы примем то, что чем на самом деле не является (хотя он может нас и удовлетворять).

##(стр 85д)

    Какие же предположения о свойствах поверхности мы делаем?

            1*. Поверхность непрерывная функция.

            2*. Поверхность гладкая функция.

            3*. У нее существует единственный оптимум.

            (Он может быть на границе). Т.е. поверхность аналитическая функция.

 

        y                                                                      y

 

                                                         x                                                                    x

Способы движения к минимуму (или максимуму функции) :

покоординатный, градиентный.

 

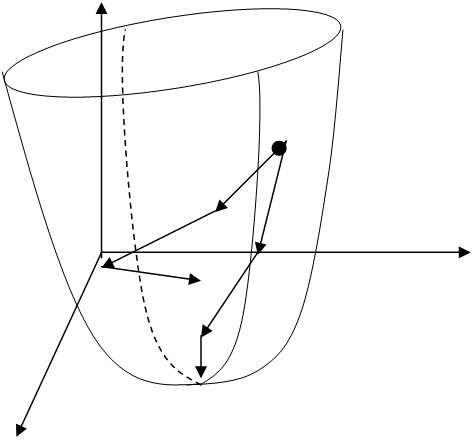Движение к минимуму носит шаговый принцип. Сначала исследуем поверхность отклика в какой-то произвольной точке (из области определения) факторного пространства. Находим направление в котором фикция убывает и движемся в том направлении. Исследуем после смещения характер функции в новой точке и движемся дальше к минимуму. Направление возрастания функции показывает ее градиент,

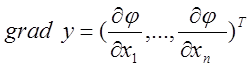
В прошлых разделах мы говорили, что удобно в качестве модели выбирать полиномиальные функции от факторов.

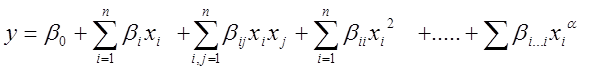
где - неизвестна

##(стр 85г)

Если априори известно, что лучше выбрать другую модель, то это следует сделать, но полиномиальная модель всегда справедлива.

Эксперименты можно разделить на экстремальные и описательные. Пока мы находимся в дали от экстремума, то имеет смысл ставить экстремальные эксперименты, чтобы двигаться к оптимуму. Но вот мы достигли почти стационарной области, где движение по градиенту не столь эффективно. Чем принципиально отличаются эти  эксперименты

В экстремальных экспериментах модель можно выбрать линейной относительно факторов.