![]() .
.
Из данной предполагаемой
модели и таблицы 3 можно получить систему из ![]() уравнений
уравнений
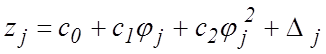 ,
, ![]() , (23)
, (23)
где ![]() – ошибки наблюдений
– ошибки наблюдений ![]() распределение по нормальному закону
с нулевым математическим ожиданием и дисперсиями
распределение по нормальному закону
с нулевым математическим ожиданием и дисперсиями 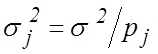 .
Из уравнений (23) необходимо найти оценки коэффициентов регрессии
.
Из уравнений (23) необходимо найти оценки коэффициентов регрессии ![]() ,
, ![]() ,
, ![]() . В такой постановке задача (23)
совпадает с задачей (18) из раздела 3.3, когда
. В такой постановке задача (23)
совпадает с задачей (18) из раздела 3.3, когда ![]() .
Для ее решения необходимо составить матрицу плана эксперимента
.
Для ее решения необходимо составить матрицу плана эксперимента ![]() размера
размера ![]() .
.
Теперь для расчета коэффициентов регрессии можно воспользоваться (8), но существует другой метод вычисления, применяемый для матриц плана эксперимента, значения элементов которых сильно отличаются по абсолютной величине (на несколько порядков) [6,7].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-0.40 |
420.19 |
1.0 |
8 |
425.96 |
425.96 |
1.0 |
15 |
0.16 |
404.20 |
0.7 |
|
2 |
-0.36 |
423.36 |
1.0 |
9 |
424.67 |
424.67 |
1.0 |
16 |
0.20 |
398.51 |
0.7 |
|
3 |
-0.32 |
425.23 |
1.0 |
10 |
422.26 |
422.26 |
0.9 |
17 |
0.24 |
392.30 |
0.7 |
|
4 |
-0.28 |
426.16 |
1.0 |
11 |
419.94 |
419.94 |
0.9 |
18 |
0.28 |
385.87 |
0.7 |
|
5 |
-0.24 |
427.00 |
1.0 |
12 |
417.42 |
417.42 |
0.8 |
19 |
0.32 |
379.00 |
0.7 |
|
6 |
-0.20 |
427.46 |
1.0 |
13 |
413.48 |
413.48 |
0.8 |
20 |
0.36 |
371.15 |
0.6 |
|
7 |
-0.16 |
427.35 |
1.0 |
14 |
408.54 |
408.54 |
0.8 |
21 |
0.40 |
363.12 |
0.6 |
Таблица 3.
|
1 |
– 0.40 |
0.1600 |
– 1.6116 |
1.89098 |
0.5174 |
|||
|
1 |
– 0.36 |
0.1296 |
– 1.4505 |
1.32350 |
0.6733 |
|||
|
1 |
– 0.32 |
0.1024 |
– 1.2893 |
0.81576 |
0.7653 |
|||
|
1 |
– 0.28 |
0.0784 |
– 1.1282 |
0.36774 |
0.8110 |
|||
|
1 |
– 0.24 |
0.0576 |
– 0.9670 |
– 0.02053 |
0.8524 |
|||
|
1 |
– 0.20 |
0.0400 |
– 0.8058 |
– 0.34908 |
0.8750 |
|||
|
1 |
– 0.16 |
0.0256 |
– 0.6447 |
– 0.61788 |
0.8696 |
|||
|
1 |
– 0.12 |
0.0144 |
– 0.4835 |
– 0.82696 |
0.8012 |
|||
|
1 |
– 0.08 |
0.0064 |
– 0.3223 |
– 0.97629 |
0.7378 |
|||
|
1 |
– 0.04 |
0.0016 |
– 0.1612 |
– 1.06590 |
0.6192 |
|||
|
|
1 |
0.00 |
0.0000 |
; |
0.0000 |
– 1.09576 |
; |
0.5051 |
|
1 |
0.04 |
0.0016 |
0.1612 |
– 1.06590 |
0.3812 |
|||
|
1 |
0.08 |
0.0064 |
0.3223 |
– 0.97629 |
0.1874 |
|||
|
1 |
0.12 |
0.0144 |
0.4835 |
– 0.82696 |
– 0.0556 |
|||
|
1 |
0.16 |
0.0256 |
0.6447 |
– 0.61788 |
– 0.2690 |
|||
|
1 |
0.20 |
0.0400 |
0.8058 |
– 0.34908 |
– 0.5489 |
|||
|
1 |
0.24 |
0.0576 |
0.9670 |
– 0.02053 |
– 0.8543 |
|||
|
1 |
0.28 |
0.0784 |
1.1282 |
0.36744 |
– 1.1706 |
|||
|
1 |
0.32 |
0.1024 |
1.2893 |
0.81576 |
– 1.5085 |
|||
|
1 |
0.36 |
0.1296 |
1.4505 |
1.32350 |
– 1.8946 |
|||
|
1 |
0.40 |
0.1600 |
1.6116 |
1.89098 |
– 2.2895 |
Сформируем вспомогательные
нормированные матрицу ![]() размера
размера ![]() и вектор
и вектор ![]() длины
длины ![]() . Для этого вычислим выборочные
средние значения и дисперсии во всех столбцах матрицы
. Для этого вычислим выборочные
средние значения и дисперсии во всех столбцах матрицы ![]() (кроме
первого) и у вектора зависимой переменной
(кроме
первого) и у вектора зависимой переменной ![]() :
:
![]() ,
, 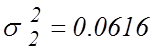 ,
, 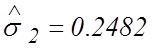 ;
;
![]() ,
, 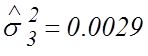 ,
, 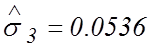 ;
;
![]() ,
, 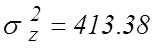 ,
, ![]() .
.
Теперь рассчитаем элементы
матрицы ![]() и вектора
и вектора ![]() по
формулам
по
формулам
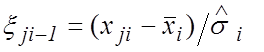 ,
, 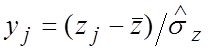 ,
, ![]() ,
,
где ![]() и
и ![]() элементы
матрицы
элементы
матрицы ![]() и вектора
и вектора ![]() соответственно, а
соответственно, а ![]() и
и ![]() элементы
нормированных матрицы и вектора соответственно. Матрица
элементы
нормированных матрицы и вектора соответственно. Матрица ![]() и
вектор
и
вектор ![]() показаны рядом с матрицей
показаны рядом с матрицей ![]() .
.
Оценки коэффициентов ![]() и
и ![]() получаются
по формулам, [7]:
получаются
по формулам, [7]:
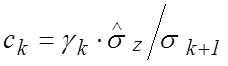 , (24)
, (24)
где вектор ![]() вспомогательных
коэффициентов
вспомогательных
коэффициентов ![]() и
и ![]() получается
из матричного соотношения, аналогичного (12),
получается
из матричного соотношения, аналогичного (12),
![]() . (25)
. (25)
Сначала рассчитаем матрицу ![]() ,
обратную матрицу
,
обратную матрицу ![]() и вектор
и вектор ![]()
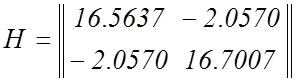 ;
; 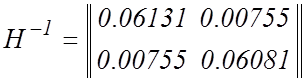 ;
; 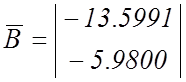 .
.
Теперь из (25) находим ![]() ,
, ![]() .
Подставляя их в (24), получаем искомые оценки коэффициентов
.
Подставляя их в (24), получаем искомые оценки коэффициентов ![]() и
и ![]() :
:
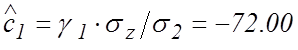 ;
; 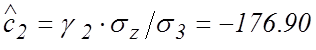 ,
,
а оценка свободного члена ![]() получается
из следующего уравнения
получается
из следующего уравнения
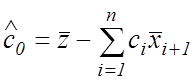 . (26)
. (26)
Подставляя в (26) значения ![]() ,
, ![]() и
и ![]() ,
имеем
,
имеем ![]() . Поэтому предполагаемая полиномиальная
модель второго порядка имеет вид
. Поэтому предполагаемая полиномиальная
модель второго порядка имеет вид
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.