Вероятностное описание погрешностей измерения, страница 13

При определении величины заряда электрона, равной  единиц CGSE, Милликен получил 58 значений величины  (в таблице 1 они обозначены через ). На основании проведенных наблюдений требуется оценить истинные значения величины заряда  и дисперсии погрешностей наблюдений .

Точечное оценивание параметров. Оценим сперва истинное значение и дисперсию погрешностей измерения величины . Тогда оценки  и  дляи  получаются умножением оценок для  на .Оценки для  обозначим соответственно  и . Они находятся по формулам (6) и (10) соответственно. Но если вычисления проводятся не на компьютере, а на калькуляторе, то их удобно делать с помощью подходящим образом выбранного числа  и очевидных равенств

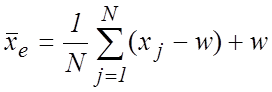,                      (16)

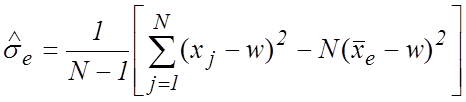.    (17)

В данном случае удобно принять . В таблице приведены значения  и 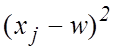. По формуле (16) имеем . Значит, оценка величины заряда равна  ед. Оценка для дисперсии погрешностей измерения величины  получается по формуле (17):

Таблица 1.

4.781	0.081	0.00656		4.771	0.071	0.00504
4.795	0.095	0.00903		4.809	0.109	0.01188
4.769	0.069	0.00176		4.790	0.090	0.00810
4.792	0.092	0.00846		4.779	0.079	0.00624
4.779	0.079	0.00624		4.788	0.088	0.00774
4.775	0.075	0.00563		4.772	0.072	0.00518
4.772	0.072	0.00518		4.791	0.091	0.00828
4.791	0.091	0.00828		4.788	0.088	0.00774
4.782	0.082	0.00672		4.783	0.083	0.00689
4.767	0.067	0.00449		4.740	0.040	0.00160
4.764	0.064	0.00410		4.775	0.075	0.00563
4.776	0.076	0.00578		4.761	0.061	0.00372
4.771	0.071	0.00504		4.792	0.092	0.00846
4.789	0.089	0.00792		4.758	0.058	0.00336
4.772	0.072	0.00518		4.764	0.064	0.00410
4.789	0.089	0.00792		4.810	0.110	0.01210
4.764	0.064	0.00410		4.799	0.099	0.00980
4.774	0.074	0.00548		4.799	0.099	0.00980
4.778	0.078	0.00608		4.797	0.097	0.00941
4.791	0.091	0.00828		4.790	0.090	0.00810
4.777	0.077	0.00593		4.747	0.047	0.00221
4.765	0.065	0.00423		4.769	0.069	0.00476
4.785	0.085	0.00723		4.806	0.100	0.01124
4.805	0.105	0.01103		4.779	0.079	0.00624
4.768	0.068	0.00462		4.785	0.085	0.00723
4.801	0.101	0.01020		4.790	0.090	0.00810
4.785	0.085	0.00723		4.777	0.077	0.00593
4.783	0.083	0.00689		4.749	0.049	0.00240
4.808	0.108	0.01166		4.781	0.081	0.00656
				Сумма	4.687	0.39209

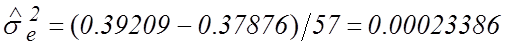;  тогда  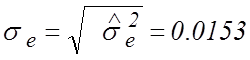 ,   а оценкой для  будет  ед.

Оценивание параметров с помощью доверительных интервалов. Найдем интервал, про который можно сказать, что он с доверительной вероятностью  накрывает оцениваемые значения параметров  и . Возьмем . По таблице распределения Стьюдента для заданных  и числа степеней свободы  находим . По формуле (13) вычисляем искомый доверительный интервал . Для той же самой доверительной вероятности   по таблице распределения 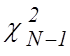 с  степенями свободы находим два числа 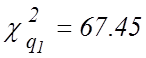 и 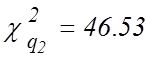  и подставляем их в (15). Получаем доверительный интервал для параметра : . Откуда вычисляем доверительный интервал для : .

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

К числу проблем, решаемых при обработке результатов измерений, относится и проверка гипотез. Задача проверки гипотез состоит в том, чтобы установить, противоречит выдвинутая гипотеза экспериментальным данным или нет. Так как результаты измерений сопровождаются случайными погрешностями, то на их основании невозможно с абсолютной достоверностью ни подтвердить, ни отвергнуть выдвинутую гипотезу, т.е. всегда существует отличная от нуля вероятность принятия ошибочного решения. Поэтому проверка гипотез осуществляется на основе статистических алгоритмов (решающих правил), а сами выдвигаемые гипотезы называются статистическими.

Пусть относительно некоторого параметра  распределения случайной величины  выдвинута гипотеза, заключающаяся в том, что его значение равно . В результате измерений получена оценка  этого параметра, на основе которой экспериментатор должен либо принять, либо отвергнуть выдвинутую гипотезу. Для этого он должен ответить на вопрос: как сильно оценка  должна отличаться от , чтобы принять или отвергнуть выдвинутую гипотезу? При этом следует учитывать, что отличие оценки  от значения  может быть вызвано, во-первых, случайным характером оценки и, во-вторых, неравенством истинного значения значению . Таким образом, если отличие  от  может быть объяснено чисто случайными причинами, то выдвинутая гипотеза принимается, в противном случае она отклоняется.