Предположим, что известна
плотность распределения  оценки
оценки ![]() . Изобразим ее графически (рис.3),
полагая, что выдвинутая гипотеза
. Изобразим ее графически (рис.3),
полагая, что выдвинутая гипотеза ![]() верна, т.е.
верна, т.е. 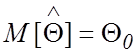 . Установим две границы
. Установим две границы ![]() и
и ![]() и
сформулируем следующее решающее правило: если
и
сформулируем следующее решающее правило: если 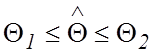 ,
то гипотеза принимается; если
,
то гипотеза принимается; если  или
или 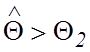 , то гипотеза отклоняется.
, то гипотеза отклоняется.
При этом может быть принято ошибочное решение, причем вероятность ошибки равна
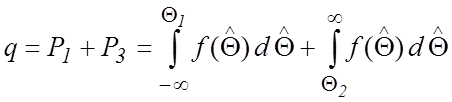 .
.
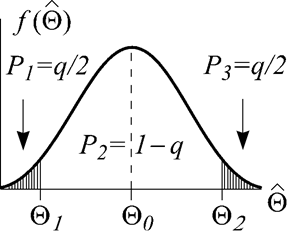
Рис. 3.
Рассмотрим другой пример
задачи проверки гипотез. Пусть некоторый параметр ![]() распределения
случайной величины может принимать только одно из двух значений:
распределения
случайной величины может принимать только одно из двух значений: ![]() или
или ![]() .
На основании экспериментально полученной оценки
.
На основании экспериментально полученной оценки ![]() необходимо
решить, какое значение
необходимо
решить, какое значение ![]() имело место в
эксперименте. В данном случае необходимо проверить гипотезу
имело место в
эксперименте. В данном случае необходимо проверить гипотезу ![]() (так называемую нулевую гипотезу)
против альтернативнай гипотезы
(так называемую нулевую гипотезу)
против альтернативнай гипотезы ![]() . На рисунке 4 изображена
плотность распределения
. На рисунке 4 изображена
плотность распределения ![]() как при условии
справедливости нулевой гипотезы
как при условии
справедливости нулевой гипотезы ![]() , так и при
условии справедливости альтернативной гипотезы
, так и при
условии справедливости альтернативной гипотезы ![]() .
.
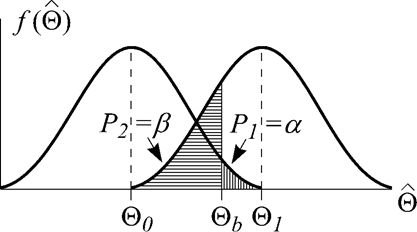
Рис. 4.
Установим границу ![]() и сформулируем решающее правило:
если
и сформулируем решающее правило:
если ![]() , то принимается нулевая гипотеза
, то принимается нулевая гипотеза ![]() ; если
; если ![]() ,
то принимается альтернативная гипотеза
,
то принимается альтернативная гипотеза ![]() .
.
Обозначим следующие вероятности:
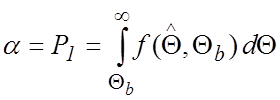 ;
; 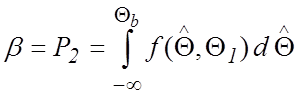 .
.
При принятии решения в соответствии с указанным решающим правилом возможны четыре ситуации:
1)
нулевая гипотеза верна, но
отклоняется. При этом имеет место ошибка 1-го рода (иногда называемая ложной
тревогой), вероятность которой равна ![]() - уровню
значимости;
- уровню
значимости;
2)
альтернативная гипотеза верна, но
отклоняется. При этом имеет место ошибка 2-го рода, вероятность которой равна ![]() ;
;
3)
нулевая гипотеза верна и
принимается. Вероятность такого события равна ![]() ;
;
4)
альтернативная гипотеза верна и
принимается. Вероятность этого равна ![]() и называется
мощностью решающего правила.
и называется
мощностью решающего правила.
Рассмотрим конкретные простейшие задачи проверки статистических гипотез.
Пусть имеется выборка ![]() (1) из
(1) из ![]() наблюдений,
причем погрешности
наблюдений,
причем погрешности ![]() удовлетворяют
предположениям 1) - 4). Положим выборочное среднее (6) равным
удовлетворяют
предположениям 1) - 4). Положим выборочное среднее (6) равным ![]() , а выборочную дисперсию (10) –
, а выборочную дисперсию (10) – ![]() (см. раздел 2). Выдвигается гипотеза
о том, что
(см. раздел 2). Выдвигается гипотеза
о том, что ![]() .
.
Как известно, величина ![]() распределена по закону Стьюдента с
распределена по закону Стьюдента с ![]() степенями свободы [1]. Поэтому
условием принятия гипотезы будет выполнение неравенства
степенями свободы [1]. Поэтому
условием принятия гипотезы будет выполнение неравенства
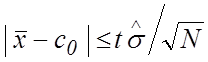 . (1)
. (1)
В случае невыполнения этого
неравенства гипотеза отклоняется. Зададимся уровнем значимости ![]() . Для вероятности
. Для вероятности ![]() и числа степеней свободы
и числа степеней свободы ![]() по таблице распределения Стьюдента
находят число
по таблице распределения Стьюдента
находят число ![]() , подставляют его в (1) и
проверяют выполнение этого неравенства. В зависимости от того, выполняется (1)
или нет, принимают или отвергают выдвинутую гипотезу.
, подставляют его в (1) и
проверяют выполнение этого неравенства. В зависимости от того, выполняется (1)
или нет, принимают или отвергают выдвинутую гипотезу.
В условиях предыдущей задачи
необходимо проверить гипотезу о равенстве дисперсии 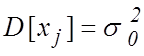 (нулевую
гипотезу).
(нулевую
гипотезу).
Как известно, величина 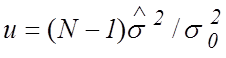 распределена по закону
распределена по закону ![]() с
с ![]() степенями
свободы [1]. Поэтому условием принятия нулевой гипотезы будет выполнение
неравенства
степенями
свободы [1]. Поэтому условием принятия нулевой гипотезы будет выполнение
неравенства
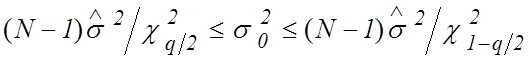 , (2)
, (2)
где 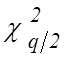 и
и 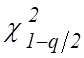 значения
величины
значения
величины ![]() из таблицы, соответствующие
вероятностям
из таблицы, соответствующие
вероятностям ![]() и
и ![]() и
числу степеней свободы
и
числу степеней свободы ![]() .Задаваясь
требуемым уровнем значимости и зная число
.Задаваясь
требуемым уровнем значимости и зная число ![]() ,
по таблице находят величины
,
по таблице находят величины 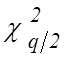 и
и 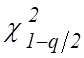 и подставляют их в (19). В случае
выполнения неравенства нулевая гипотеза о равенстве дисперсии величине
и подставляют их в (19). В случае
выполнения неравенства нулевая гипотеза о равенстве дисперсии величине ![]() принимается; если же (2) не
выполняется, то гипотеза отвергается.
принимается; если же (2) не
выполняется, то гипотеза отвергается.
Пусть по данным двух
независимых выборок наблюдений ![]()
![]() и
и ![]()
![]() получены оценки
получены оценки 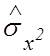 и
и 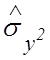 дисперсий
дисперсий
![]() и
и ![]() соответственно.
Необходимо проверить гипотезу, что
соответственно.
Необходимо проверить гипотезу, что ![]() , т.е. дисперсии
наблюдений
, т.е. дисперсии
наблюдений ![]() и
и ![]() равны.
равны.
В данном случае выбор
критерия основан на том факте, что если величины ![]() и
и
![]() распределены по нормальному закону и
взаимно независимы, то случайная величина
распределены по нормальному закону и
взаимно независимы, то случайная величина 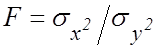 имеет
имеет
![]() -распределение Фишера, зависящее
только от целых констант
-распределение Фишера, зависящее
только от целых констант ![]() и
и ![]() [1-3]. Данное распределение
затабулировано. По двум входным величинам
[1-3]. Данное распределение
затабулировано. По двум входным величинам ![]() ,
, ![]() и уровню значимости
и уровню значимости ![]() находят величину
находят величину ![]() , которую подставляют в неравенство
, которую подставляют в неравенство
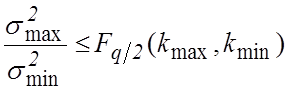 , (3)
, (3)
где индексы ![]() и
и ![]() относятся соответственно к большей
по величине и меньшей оценкам дисперсий
относятся соответственно к большей
по величине и меньшей оценкам дисперсий ![]() и
и
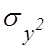 . Для того, чтобы гипотеза о
равенстве дисперсий
. Для того, чтобы гипотеза о
равенстве дисперсий ![]() и
и 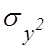 была
принята с уровнем значимости
была
принята с уровнем значимости ![]() (доверительной
вероятностью
(доверительной
вероятностью ![]() ), необходимо выполнение
неравенства (3). В противном случае данная гипотеза должна быть отвергнута в
пользу альтернативной гипотезы, что
), необходимо выполнение
неравенства (3). В противном случае данная гипотеза должна быть отвергнута в
пользу альтернативной гипотезы, что ![]() . Необходимо
помнить, что при использовании (3) с уровнем значимости
. Необходимо
помнить, что при использовании (3) с уровнем значимости ![]() в
таблице распределения Фишера выбирается число, соответствующее значению уровня
значимости
в
таблице распределения Фишера выбирается число, соответствующее значению уровня
значимости ![]() .
.
Иногда в рядах наблюдений
попадаются данные, которые на глаз резко выделяются среди других. Это может
быть случайным обстоятельством, т.к. в последовательности наблюдений
теоретически могут быть данные ![]() , сильно
уклоняющиеся в обе стороны от
, сильно
уклоняющиеся в обе стороны от ![]() , но может быть
вызвано и грубой ошибкой наблюдателя.
, но может быть
вызвано и грубой ошибкой наблюдателя.
Рассмотрим в ряду наблюдений ![]() , распределенных нормально (1) и
независимых, например, максимальное
, распределенных нормально (1) и
независимых, например, максимальное ![]() . Для того, чтобы
решить, нужно ли отбросить наблюдение
. Для того, чтобы
решить, нужно ли отбросить наблюдение ![]() как
грубую ошибку, можно воспользоваться правилом "трех сигм", но более
грамотно это следует выяснить с помощью критерия Ф. Грэббса. Для этого
нужно сформировать дробь "типа Стьюдента"
как
грубую ошибку, можно воспользоваться правилом "трех сигм", но более
грамотно это следует выяснить с помощью критерия Ф. Грэббса. Для этого
нужно сформировать дробь "типа Стьюдента"
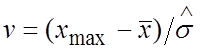 , (4)
, (4)
распределение которой зависит только от объема выборки ![]() , и оно было затабулировано Грэббсом.
По заданным
, и оно было затабулировано Грэббсом.
По заданным ![]() и доверительной вероятности
и доверительной вероятности ![]() необходимо найти в таблице Грэббса
число
необходимо найти в таблице Грэббса
число ![]() . Если окажется
. Если окажется ![]() , то
, то ![]() следует
отбросить, как наблюдение, содержащее грубую ошибку; а если
следует
отбросить, как наблюдение, содержащее грубую ошибку; а если ![]() , то
, то ![]() можно
оставить. Если подозрение вызывает минимальное из чисел
можно
оставить. Если подозрение вызывает минимальное из чисел ![]() ,
то дробь (4) следует видоизменить
,
то дробь (4) следует видоизменить
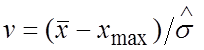 .
.
Измерение эквивалентной
электропроводности ![]() вещества
вещества ![]() при нормальной концентрации
при нормальной концентрации ![]() дали следующие результаты:
дали следующие результаты:
|
76.35 |
79.09 |
72.01 |
70.41 |
71.15 |
68.69 |
71.03 |
74.58 |
74.41 |
77.83 |
При уровнях значимости ![]() ;
; ![]() ;
;
![]() проверить гипотезы о равенстве
величины эквивалентной электропроводности значениям
проверить гипотезы о равенстве
величины эквивалентной электропроводности значениям ![]() ;
;
![]() ;
; ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.