ЗАДАЧА № 4
Цель работы: По измеренным значениям температуры и электрического сопротивления проводника определить функциональную зависимость R = f(t).
При установлении функциональной зависимости между двумя величинами может быть использован метод наименьших квадратов. В этом методе оценки параметров зависимости определяют из условия, что сумма квадратов отклонений расчетных значений аппроксимирующей функции от экспериментальных значений должна быть минимальной.
Теоретическая зависимость Rt = f(t) имеет вид:
Rt = Ro(1 + a t) , (1)
где Ro – значение сопротивления проводника при 0 оС; a ‑ температурный коэффициент сопротивления проводника; t – температура.
Rt = A + Bt , (2)
где А = Ro; В = Ro a. График функции у = А + Вх ‑ прямая линия с наклоном В, пересекающая ось ординат в точке А (рис.1).
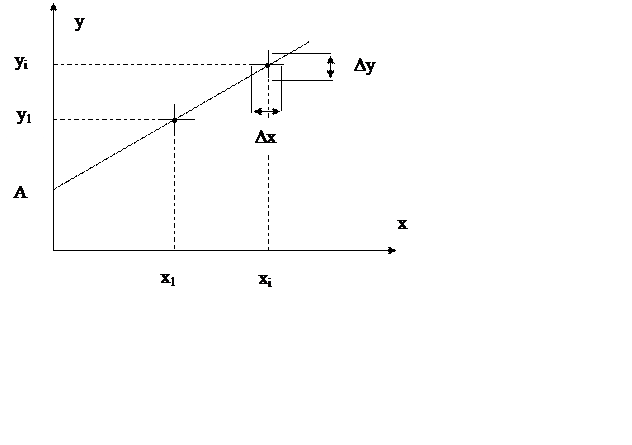 |
Рис.1 График линейной зависимости.
Экспериментальные точки в общем случае должны находиться в поле прямоугольника со сторонами, соответствующими интервалам, в которых находятся значения xi и yi (Dх и Dу).
При использовании метода наименьших квадратов предполагается, что:
- значения аргумента xi известно точно;
- все поправки на известные систематические эффекты введены, неопределенность определения значения yi зависит только от случайных эффектов (возмущающих факторов).
Выражения для расчета оценок постоянных:
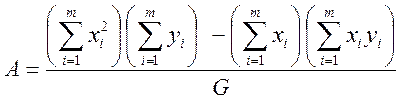 (3)
(3)
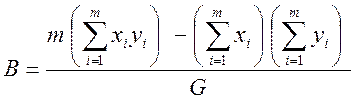 (4)
(4)
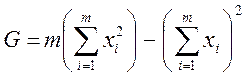 (5)
(5)
m – число точек, полученных при измерении.
Постоянные А и В определяются с некоторой неопределенностью. Мерой этой неопределенности является стандартное отклонение.
Для постоянной А:
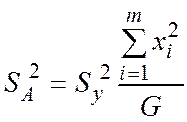 (6)
(6)
Для постоянной В:
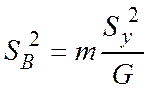 (7)
(7)
Стандартное отклонение, характеризующее неопределенность, с которой определяются значения yi, определяется согласно выражению:
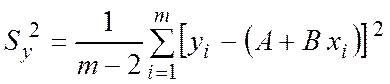 (8)
(8)
|
t, oC |
10 |
20 |
30 |
40 |
|
Rt, Ом |
10,3 |
10,9 |
11,3 |
11,6 |
1. Согласно (3‑5) и с учетом (2) вычисляются значения А и В;
2. Согласно (6,7) вычисляются значения SA, SB;
3. Значение SR вычисляется согласно (8)
3.3. Рисуется график, на котором строится зависимость Rt = A + Bt, а также указываются полученные экспериментально точки и интервалы, в которых находятся значения Rti.
3.4. Выражение Rt = A + Bt приводится к виду Rt = Ro(1 + a t).
Вычисления провести “В ручную” и с использованием Microsoft Office Excel. Сделать выводы с точки зрения метрологической аттестации разработанного ПО на основе Excel.
Решение
1. Вычислим значения А и В согласно (3-5):
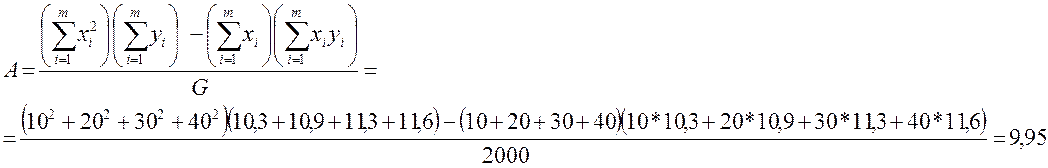
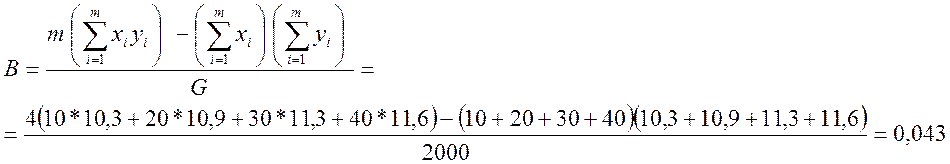
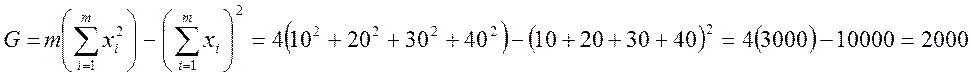
2. Согласно (6,7) вычислим стандартное отклонение для значении А и В:
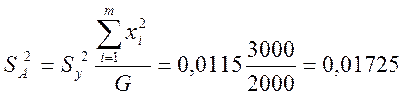
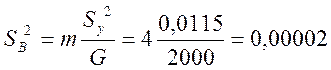
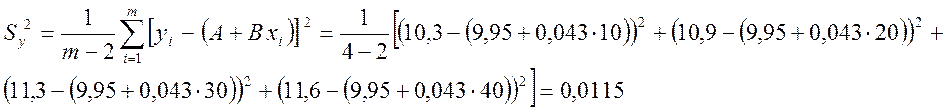
SA=0,131339; SB=0,004796; Sy=0,107238
3. Построим график зависимости Rt = A + Bt (рис.2), указав полученные экспериментально точки и интервалы:
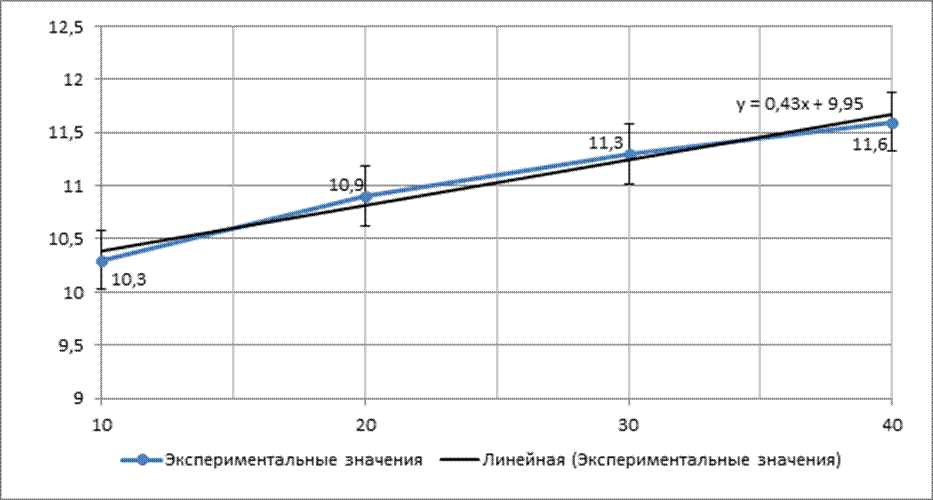
Рис. 2. График зависимости Rt = A + Bt
4. Выражение Rt = A + Bt приведем к виду Rt = Ro(1 + a t).
Где Ro=А; a=В/R0, А=9,95; В=0,043:
Rt=9,95(1+0,043/9,95t)
Rt=9,95(1+0,0043t).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.