Разработка ионно-плазменной технологической установки для нанесения функционального покрытия на крышки масляных фильтров, страница 38

where b=0.9 – we accept constant for technical calculations, Р_ср=1.125·10^-2 torr.

Solving this equation for d, we shall receive d=1.8 sm. Considering, that diameter of an entrance branch pipe of the pump = 6.3 sm more the than received diameter, structurally we accept , then conductivity at the pump input is equal to infinity. We determine conductivity of pipelines adjusted for diameter from expression (4.21):

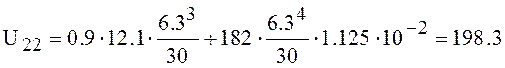 l/s,

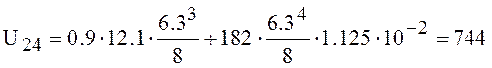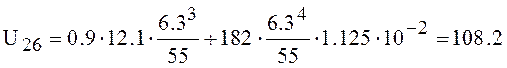 l/s,

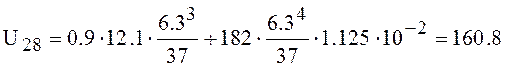 l/s,

 l/s.

Conductivity of boot is defined as conductivity of the pipeline with length l₅  (4.25):

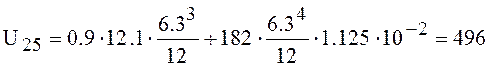 l/s

Then the general conductivity of the section from pumped out object up to the vacuum pump:

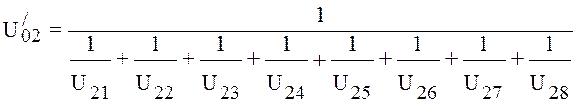,           (4.26)

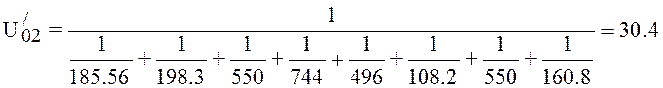 l/s.

The use factor of the vacuum pump is equal:

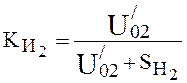,                                               (4.27)

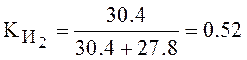
 hence the system is calculated correctly.

Pressure distribution on length of the pipeline is calculated. Effective pump speed, by formula (4.17):

,

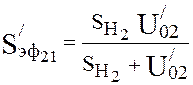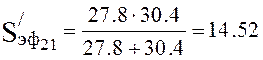 l/s.

Limiting pressure of the vacuum pump = 1,125·10^-2 torr. Pressure at the beginning of the first section is defined by expression:

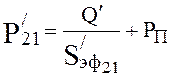,                                                           (4.28)

 torr.

Conductivity of the first section is defined by expression:

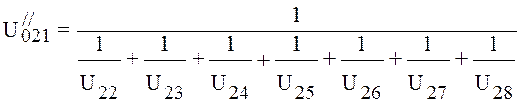,          (4.29)

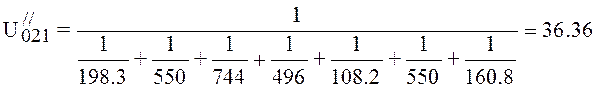 l/s.

Effective pump speed (4.17):

,

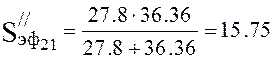 l/s.

Pressure at the end of the first section (4.20):

,

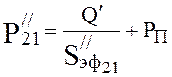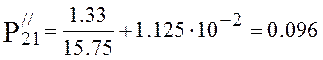 torr.

Pressure at the beginning of the second section . Conductivity of the second section is defined from expression:

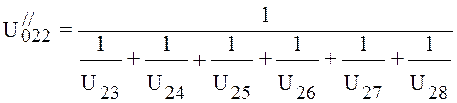,                     (4.30)

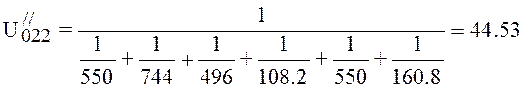 l/s.

Effective pump speed (4.17):

,                                                    

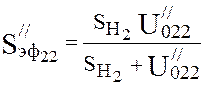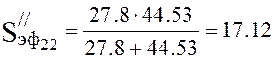 l/s.

Pressure at the end of the second section (4.20):

,

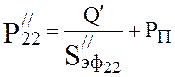 torr.

Pressure at the beginning of the third section . Conductivity of the third section is defined from expression:

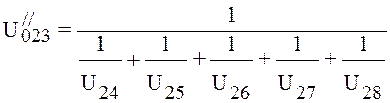,                                (4.31)

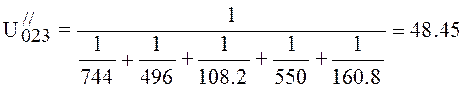 l/s.

Effective pump speed (4.17):

,                                                     

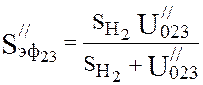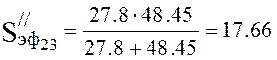 l/s.

Pressure at the end of the third section (4.20):

,

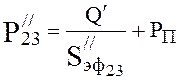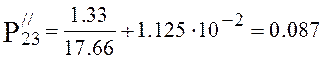 torr.

Pressure at the beginning of the fourth section . Conductivity of the fourth section is defined from expression:

,                                           (4.32)

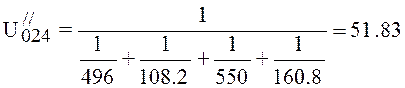 l/s.

Effective pump speed (4.17):

,                                                    

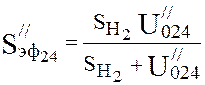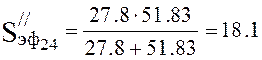 l/s.

Pressure at the end of the fourth section (4.20):

,

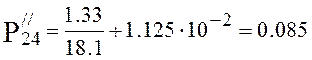 torr.

Pressure at the beginning of the fifth section . Conductivity of the fifth section is defined from expression:

,                                            (4.33)

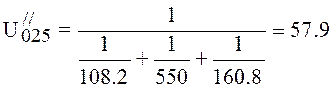 l/s.

Effective pump speed (4.17):

,                                                    

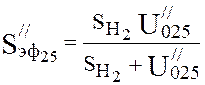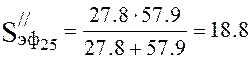 l/s.

Pressure at the end of the fifth section (4.20):

,

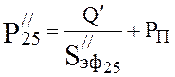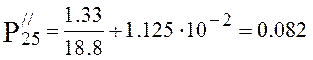 torr.

Pressure at the beginning of the sixth section . Conductivity of the sixth section is defined from expression:

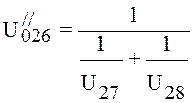,                                                       (4.34)

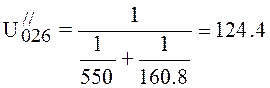 l/s.

Effective pump speed (4.17):

,                                                    

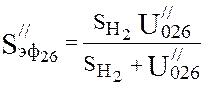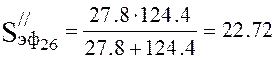 l/s.

Pressure at the end of the sixth section (4.20):

,

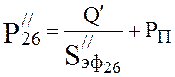 torr.

Pressure at the beginning of the seventh section . Conductivity of the seventh section is defined from expression:

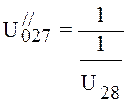,                                                        (4.35)

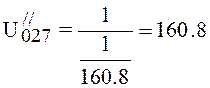 l/s.

Effective pump speed (4.17):

,                                                    

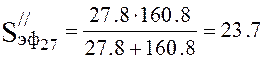 l/s.

Pressure at the end of the seventh section (4.20):

,

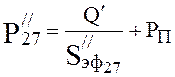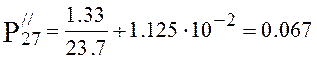 torr.

Pressure at the beginning of the eighth section . Conductivity of the pipeline is equal to infinity. Pressure at the end of the eighth section is found under the formula (4.20):

,

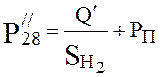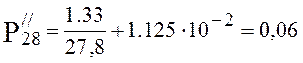 torr.

The received pressure values we put in the table and build the schedule of pressure  distribution on the pipeline length of the second section of vacuum system.

Table 4.4. Pressure distribution  on the pipeline  length of the second section of vacuum system