Разработка ионно-плазменной технологической установки для нанесения функционального покрытия на крышки масляных фильтров, страница 22

We shall calculate distance from the cathode up to the conditional anode in MAS for the discharge in nitrogen [14]:

X₀²=2×m_e×U_p²/W₀×B²,                                              (3.1)

where m_e=9,1×10^{-31 kg} – electron mass,

W₀- total energy spent by electron on one act of ionization.

Calculation of W₀ is inconvenient and usually experimental data are used. For nitrogen  W₀=2,33×10^-18 joule/ion.

X₀²=2×9,1×10^-31×600²/(2,33×10^-18×0,1²),

X₀=0,0053 m.

Real anode of MAS should be located from the center of dispersion zone on distance greater, than there is a conditional anode.

Expression for current-voltage characteristic of discharge looks like [14]:

I=C(U²-1.5×U×U₀-0.5×U₀²);                                             (3.2)

С=N(p+D);                                                          (3.3)

N=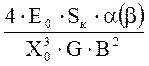;                                                        (3.4)

D=(S_c/S_n)×G×B;                                                      (3.5)

G=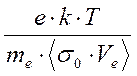;                                                (3.6)

where U₀- minimal potential at which the discharge exists (discharge quenching potential), depending on working gas  pressure and value of magnetic field induction, V;  C, N, D- factors depending on  magnetic field induction; S_к – the area of sprayed cathode surface, m²; a(b)- parameter defining change of classical electron mobility in magnetic field; S_с и S_n- areas of section of plasma toroid and its surface accordingly; T- working gas temperature, K; S_k=0,012 m², е=1,6×10^{-19 C}, k=1,38×10^-23 joule/К, Т=400 К, <s×V_e>=10^-12 m³/s, e₀=8,85×10^-12 farad/m, a(b)=1, S_c/S_n=0,25; p=0,133 P.

G=;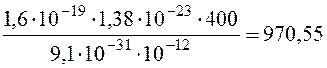

N=;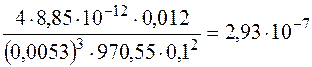

D=0,25×970,55×0.1=24,26;

С=2,93×10^-7(0,133+24,26)=7,17×10^-6.

We substitute the received factor in the formula (3.2) and find the discharge current:

I=7,17×10^-6(600²-1,5×600×325+0,5×325²)=0,86 A.

The current density  we define under the formula:

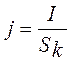          ,                                                                    (3.7)

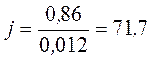 A/m².               

For the quantitative characteristic of materials dispersion process use concept of dispersion speed defined by thickness of a material superficial layer, deleted in unit of time. According to definition the dispersion speed can be written down as

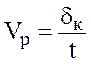,                                                                (3.8)

where δ_к – thickness of the sprayed layer; t – time of dispersion.

At designing of atomizing systems with the set productivity it is necessary to be able to count in advance dispersion speed of various materials at used energy and ions current density. For calculation of dispersion speed of materials at normal falling of ions the formula [16] is received:

, nm/s,                                       (3.9)

where A - atomic weight of sprayed material, g/mole; N_A – Avogadro constant, atom/mole; ρ – material density, g/sm³, S - factor of material dispersion, atom/ion; j_и – density of ionic current in section, perpendicular to the direction of ions falling, А/sm².

The value S_об.=SּA/(N_Aּρ) represents factor of volumetric dispersion, sm³/ion. Thus, the formula (4.9) becomes:

,                                      (3.10)

In our case for titan S_об. makes 2,15ּ10^-23 sm³/ion [16]. Then finally we define the dispersion speed:

 nm/s.

Dispersion speed of the target material  is equal 9,63 nm/s.

We shall define, what part of a sprayed material is besieged on a substrate. Under condition of uniform dispersion of a material in all directions equality takes place:

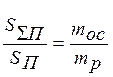,                                                            (3.11)

where  - the total area of a covers surface on which the coating is besieged;

 - the area of a conditional cylindrical surface on which the sprayed particles would be besieged all, passing through filters covers axes of rotation;

m_р, m_ос – weight of the material sprayed and besieged on the filters covers.