Математика \ Математика

Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 9

                                                            Z

A3   z                       

A

O             A2       Y

                           y

A1

x                B

X

Рис. 10

Таким  образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором  можно связать три числа  (или два числа , если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.

ОПРЕДЕЛЕНИЕ. Координатами вектора  в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.

Таким образом, можно дать еще одно определение вектора.

ОПРЕДЕЛЕНИЕ. Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).

ПРИМЕР. Если  ,  то  =(2,3,4)  и  наоборот,  если , то

Так  как, с одной стороны, вектор  – объект, имеющий длину и направление, а с другой, – упорядоченная  тройка  чисел,  то,  зная  длину  и  направление,  можно  определить  его  координаты  и  наоборот.  Направление  вектора  в  заданной  системе  координат  характеризуется  его  направляющими  косинусами (рис. 11):

.

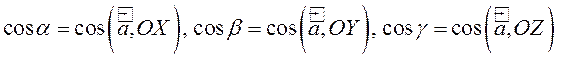Пусть                                                                

                     Z

                

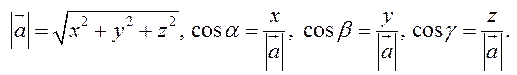
O      

                         Y

X

Рис. 11

Из этих формул очевидно следует основное свойство направляющих косинусов:  

Если известны длина   и направляющие косинусы вектора, то его координаты вычисляются по формулам:     

            z

O                           y

x

Рис. 12

Пусть  – произвольный вектор в системе OXYZ,  – радиус-векторы его начала и конца, 

, (рис.12).

Тогда     

 (см. свойства линейных операций над векторами). Таким образом, , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.

ОПРЕДЕЛЕНИЕ. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).

                              

           

Рис. 13

Если  – базис, то  – другой базис, так как изменился порядок следования векторов.

         ОПРЕДЕЛЕНИЕ. Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.

Такой базис принято обозначать  .

Из теоремы 2 следует, что всякий вектор    может быть разложен по базису , то есть представлен в виде: . Числа  называются координатами    в базисе  .

ОПРЕДЕЛЕНИЕ. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.

Если   – базис, то представление вектора в виде   называется разложением    по базису  и  – координаты   в этом базисе.

ОПРЕДЕЛЕНИЕ.  Базисом на прямой называется любой ненулевой вектор этой прямой.

ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ

Рассмотрим задачу: дан отрезок  . Найти точку , которая делит   в заданном отношении  :  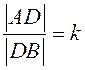(рис. 14).   

                              z

                              A        D

                                                 B

                              О                             y

x

Рис. 14

Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда   

Обозначим

 

Так как  (лежат на одной прямой) и , то 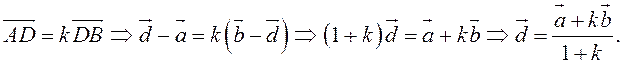 Переходя от этого векторного  равенства к равенству соответствующих координат, получим: 

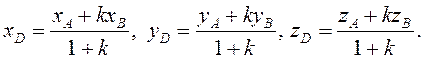                                  (2.3)

ЗАМЕЧАНИЕ 1. Если  – середина отрезка , то , поэтому

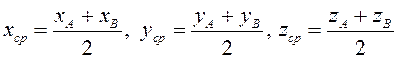                                   (2.4)

ЗАМЕЧАНИЕ 2.  Если ,  , то точка  лежит за пределами : так как , то при   

                                   D

B 

A

Рис. 15

В этом случае 

Пусть

 (рис. 15).

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ.  Скалярным произведением векторов   и  называется скаляр (число), равный  .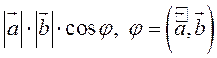

Скалярное произведение обозначается так:     или .

Рис. 16

Так как   (рис. 16) или , то  .      

Скачать файл