Математика \ Математика

Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 15

Считая, что  из (3.18) получим, что 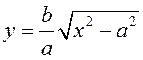 – уравнение части гиперболы, расположенной в первой четверти. Заметим, что при неограниченном возрастании  разность  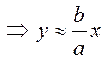 , то есть при достаточно больших   гипербола приближается к прямой 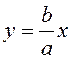, причем ординаты точек на ней меньше соответствующих ординат точек на этой прямой: 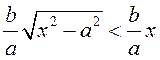. Прямая 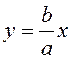 называется асимптотой гиперболы.

   У

b

-c  -aО a       c           Х

-b

Рис. 31

Из симметрии гиперболы следует, что то же самое происходит во второй, третьей и четвертой  четвертях. Поэтому  – также асимптота.

Итак, прямые  – асимптоты гиперболы (3.18), а гипербола – кривая, состоящая из двух ветвей (рис. 31).

Если фокусы гиперболы лежат на , то ее уравнение имеет вид:

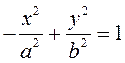                                                    (3.19)

Гиперболы (3.18) и (3.19) называются сопряженными (рис. 31). Уравнения асимптот  (3.19) такие же, как и для (3.18), но действительной является ось .

Если , то гипербола называется равносторонней:   – уравнения ее асимптот (рис. 32 ).   

                                    У

-aОa              x

Рис. 32

Очевидно, в этом случае асимптоты перпендикулярны. После поворота осей координат на  против часовой стрелки, получим  гиперболу, задаваемую уравнением  .

ЗАМЕЧАНИЕ 1. Если центр гиперболы  в точке , а оси симметрии параллельны координатным осям, то уравнение гиперболы имеет вид       

.           (3.20)

ЗАМЕЧАНИЕ 2. К кривым второго порядка гиперболического типа относится также  пара пересекающихся прямых:  .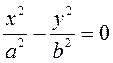

ПРИМЕР. Найти координаты центра и написать уравнения асимптот гиперболы   .

Приведем данное уравнение к виду (3.20):

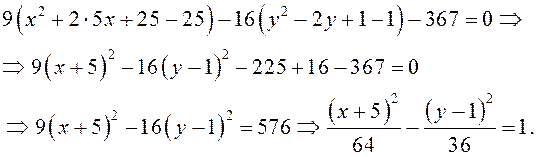
Таким образом,  – центр, а 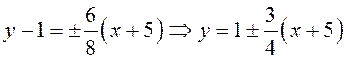 – уравнения асимптот данной гиперболы.

Парабола

ОПРЕДЕЛЕНИЕ. Парабола – совокупность точек плоскости, равноудаленных от фиксированной точки этой плоскости, называемой фокусом, и фиксированной прямой, не проходящей через эту точку, называемой директрисой. 

Чтобы вывести уравнение параболы, выберем пдск следующим образом: ось абсцисс проведем через фокус перпендикулярно директрисе, а ось ординат посередине между фокусом и директрисой (рис. 33).

Пусть расстояние между фокусом  и директрисой  равно . Тогда 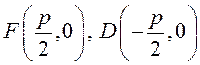. Если  – произвольная точка на параболе, то по определению

                                 y

K                      M

D    О       F               x

Рис. 33

.                 (3.21)

(3.21) – уравнение параболы в выбранной системе координат.

Упростим его:                               

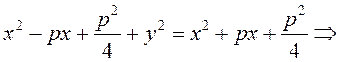
,                                                       (3.22)

(3.22) – каноническое уравнение параболы;  называется ее параметром.

Из уравнения следует, что парабола симметрична относительно   и проходит через начало координат. Кроме того,  если , то , поэтому кривая лежит в правой полуплоскости и с ростом величины   также растет. Точка пересечения параболы с осью симметрии называется ее вершиной (рис. 34).

                                 y

   

О      F                 x

                                y

F          О                       x

Рис. 34

Если фокус параболы на оси ОУ (рис. 35), то ее каноническое уравнение имеет вид  .

                               y

F

О                      x

                             y

О                     x

F

Рис. 35

ЗАМЕЧАНИЕ 1. Если вершина параболы в точке   и ось симметрии параллельна , то ее уравнение имеет вид  .

ЗАМЕЧАНИЕ 2.  К кривым второго порядка параболического типа относятся также   – пара совпадающих прямых;   – пара параллельных прямых;   – пара мнимых параллельных прямых.

ПРИМЕР. Написать уравнение геометрического места точек, равноудаленных от прямой   и точки .

По определению множество точек, равноудаленных от данных точки и прямой, является параболой. Пусть  – произвольная точка искомой параболы, тогда 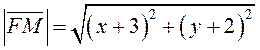. Расстояние от точки  до прямой  вычисляется по формуле (3.8): 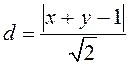. Из условия следует, что

Скачать файл