Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 6

1) умножение любой строки на число ;

2) перемена местами двух строк;

3) прибавление ко всем элементам строки  соответствующих элементов другой строки, умноженных на одно и то же число;

4)  отбрасывание нулевой строки;

5)  отбрасывание одной из двух пропорциональных строк;

6) те же преобразования со столбцами.

ТЕОРЕМА. Элементарные преобразования не изменяют ранга матрицы. С их помощью всякую матрицу можно привести к диагональному виду, и ее ранг равен количеству ненулевых элементов на главной диагонали (без доказательства).

Покажем теперь, что ранг матрицы F из последнего примера равен 2.

.

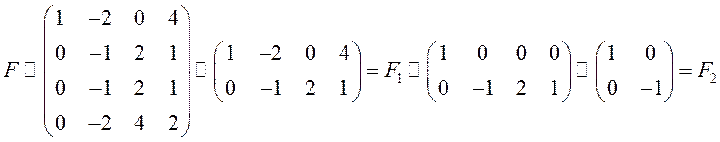При переходе от  к  и  использовались элементарные  преобразования  3), 5), 6): первую строку прибавили ко второй и четвертой, затем отбросили две из трех пропорциональных строк; далее первый столбец  прибавили ко второму и четвертому с коэффициентами 2 и (-4) соответственно и два из трех пропорциональных столбцов отбросили. По теореме .

Вычислить , очевидно, можно было, получив лишь матрицу , не выполняя дальнейших преобразований.

ИССЛЕДОВАНИЕ  ПРОИЗВОЛЬНЫХ  СИСТЕМ 

ЛИНЕЙНЫХ  УРАВНЕНИЙ

Рассмотрим систему  m линейных уравнений с n неизвестными.

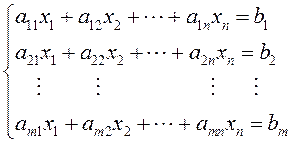                                     (1.14)

Матрица 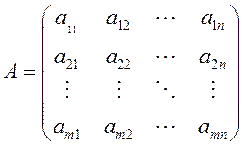   называется основной матрицей системы (1.14), а   

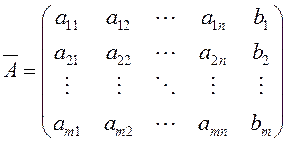  – расширенной матрицей системы (1.14).

ОПРЕДЕЛЕНИЕ. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.

ОПРЕДЕЛЕНИЕ. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного.

ПРИМЕР.

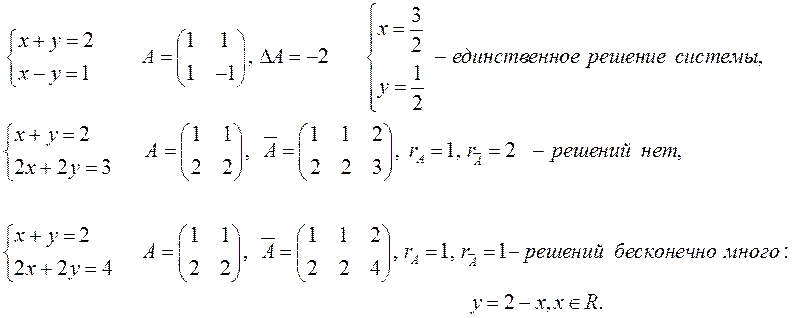
ТЕОРЕМА. (Кронекера-Капелли, критерий совместности системы линейных уравнений)   Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен  рангу расширенной (без доказательства).

ТЕОРЕМА (о числе решений). Пусть выполнены условия совместности системы линейных уравнений. Тогда, если , где  – число неизвестных, то система имеет единственное решение. Если , то система имеет  бесконечное множество решений, при этом  () переменных задаются свободно, тогда оставшиеся  переменных определятся единственным образом (без доказательства).

ОДНОРОДНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Система линейных уравнений вида

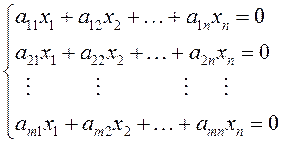                                            (1.15)

называется однородной.

Однородная система всегда совместна, так как   – ее решение. Такое решение называется нулевым или тривиальным.

ТЕОРЕМА. Для того чтобы система линейных однородных уравнений (1.15) имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы    был меньше числа неизвестных  .

ДОКАЗАТЕЛЬСТВО.

1) Достаточность:  (1.15) имеет нетривиальное решение.

По теореме о числе решений система  в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.

2) Необходимость: (1.15) имеет нетривиальное решение .

Пусть , тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно  и .

СЛЕДСТВИЕ. Для того чтобы однородная система   уравнений  с   неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.

ДОКАЗАТЕЛЬСТВО.

1) Достаточность:  система имеет нетривиальное решение.

Так как единственный минор -го порядка равен нулю, то , значит, нетривиальное решение существует.

2) Необходимость: система имеет нетривиальное решение .

Если , то не равен нулю минор -го порядка основной матрицы, значит,   и решение единственно, что противоречит условию.

МЕТОД   ГАУССА

Этим методом можно решить любую систему линейных уравнений (1.14) или доказать, что она несовместна. Он состоит в  последовательном исключении неизвестных системы (1.14) по следующей схеме: выписывается расширенная матрица системы  и приводится  к наиболее простому виду – треугольному или виду трапеции – с помощью следующих преобразований над ее  строками:

1) перемена местами двух строк  (уравнений);