Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 18

Предположим, что уравнение   задает в пдск ХОУ эллипс. Если , то это уравнение не является каноническим уравнением эллипса, а потому, хотя О(0, 0) – его центр, оси симметрии не совпадают с ОХ и ОУ (рис. 43). Тем не менее, заметим, что если оси системы  повернуть на

Пусть                                               .

Вычислим       

.

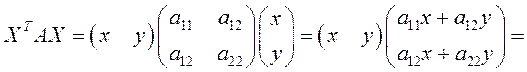
Таким образом, квадратичная форма может быть записана в матричном виде:

                                                                                               (3.31)

Пусть  – координаты точек плоскости в системе , а  – координаты точек плоскости  в новой системе , где кривая задается каноническим уравнением. Переход от “старых” координат к “новым” будем искать в виде

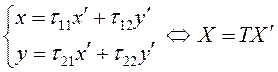.                                    (3.32)

(3.32) – ортогональное линейное преобразование с матрицей

; .

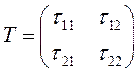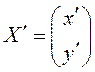По определению ортогональной матрицы

                                                                                                                 (3.33)

(В результате ортогонального преобразования не происходит изменение площадей фигур, то есть фигуры не деформируются.)

Чтобы узнать, как изменится матрица квадратичной формы в результате линейного преобразования (3.32), подставим (3.32) в (3.31):   (свойство 5 умножения матриц) (свойство 2 умножения матриц и равенство (3.33)) – матрица новой квадратичной формы.

Так как в “новой” системе координат кривая должна задаваться каноническим уравнением, то есть в нем должно отсутствовать произведение координат , то  имеет вид: 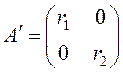 , где  – неизвестные числа. Умножим равенство  на матрицу  слева. Так как  , то получим:

.

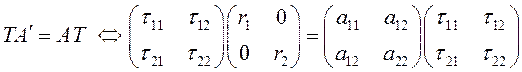По определению равных матриц имеем:

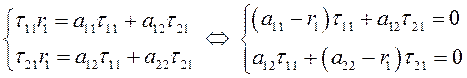                         ,                    (3.34)

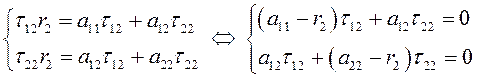                        .                    (3.35)

Системы уравнений (3.34), (3.35) – линейные и однородные. Они имеют нетривиальное решение, если их определители равны 0.

.

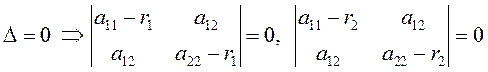Это означает, что   и  являются решениями уравнения

.                                (3.36)

Уравнение (3.36) называется характеристическим уравнением матрицы  (характеристическим уравнением квадратичной формы). Его решения  и  называются собственными значениями матрицы  (квадратичной формы).

Покажем, что дискриминант квадратного уравнения (3.36) положителен, то есть любая квадратичная форма двух переменных имеет 2 различных собственных значения.

Вычислим определитель (3.36):    

.

Дискриминант   , так как  (иначе квадратичная форма будет канонической).

Таким образом, коэффициентами при  и  в каноническом виде квадратичной формы являются ее собственные значения, то есть решения уравнения (3.36).

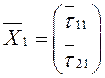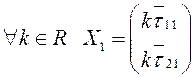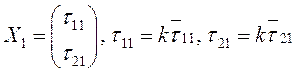Решим (3.36) и подставим  в (3.34). Система имеет бесконечное множество решений и пусть  – одно их них. Так как система (3.34) однородная, то  – тоже решение. Подберем  так, чтобы вектор   был единичным: .

Векторы  и   называется собственными векторами квадратичной формы, соответствующими собственному значению , или первыми собственными векторами. Их направление называется первым главным направлением квадратичной формы. Таким образом, первым собственным вектором квадратичной формы называется любое ненулевое решение системы (3.34).

Аналогично подставим  в (3.35) и найдем 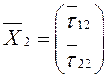  – второй собственный вектор, соответствующий собственному значению . Его направление называется вторым главным направлением квадратичной формы. 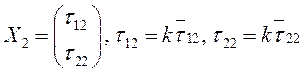  – второй единичный собственный вектор, то есть .

Можно показать, что . Кроме того,   – первый собственный вектор, а 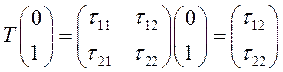  – второй собственный вектор, поэтому ортами “новой” системы координат , к которой мы перейдем в результате линейного преобразования с матрицей , являются единичные собственные векторы квадратичной формы, найденные как решения систем (3.34), (3.35). Направив оси “новой” системы координат вдоль собственных векторов  и , получим систему координат,  в которой квадратичная форма будет иметь канонический вид .