Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 10

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

1.  – очевидно из определения.

2.

Доказательство: 

3.    

Доказательство:

а)  – очевидно.  б)     

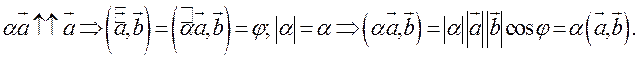
в)  В этом случае  

4. .

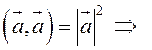
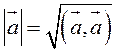Отсюда следует, что 

Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:

5.  

Доказательство:

а) пусть  

б) пусть  или , или .

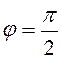В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что . В третьем случае  или 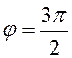, то есть .

Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов  :

Пусть в некоторой пдск . Найдем скалярное  произведение этих векторов:

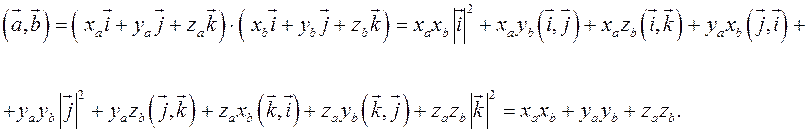
Таким образом,                                                             (2.5)

ПРИМЕР. Найти, при каком значении  векторы  перпендикулярны.

Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 

ПРИМЕР. Найти угол между биссектрисой   и медианой , если

Так как                                          ,      

то 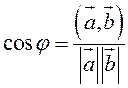                                                   .                                                   (2.6)

Найдем координаты векторов  и . Точка  – середина ,  поэтому по формулам (2.4) .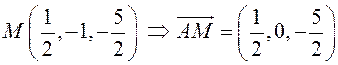

По теореме о биссектрисе внутреннего угла треугольника 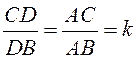 . Чтобы найти , вычислим длины  и :

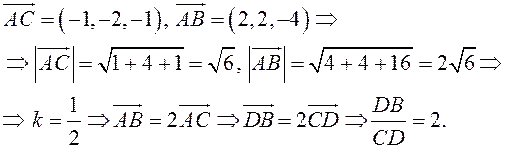
Разделим отрезок  в данном отношении по формулам (2.3):

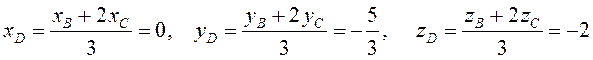, отсюда                                  .

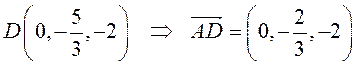Заметим, что 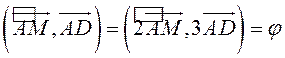 . Это замечание позволит нам не иметь дело с дробями, так как   

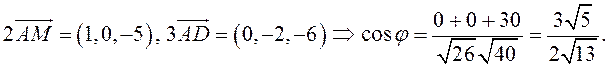
ПРИМЕР.  Найти   , если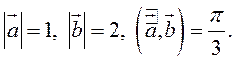 

Воспользуемся свойствами 1–4 скалярного произведения:

.

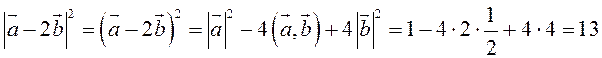Отсюда  

ЗАМЕЧАНИЕ. Так как работа силы  по перемещению материальной точки вдоль вектора  вычисляется по формуле , то  .

ВЕКТОРНОЕ  ПРОИЗВЕДЕНИЕ  ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ.  Тройка  некомпланарных векторов , имеющих общее начало, называется правой (левой), если с конца третьего вектора   вращение первого вектора  ко второму вектору  по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).

Рис. 17	– левая тройка,  – правая тройка,  – левая тройка.
Рис. 18	– правая тройка (рис. 18).

ОПРЕДЕЛЕНИЕ. Векторным произведением вектора  на вектор  называется вектор , удовлетворяющий условиям:

1.   ( перпендикулярен плоскости векторов   и ).

2. Направление   таково, что тройка  – правая.

3. .

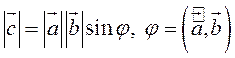Векторное произведение обозначается так:  или .

ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.

.

Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.

Заметим, что

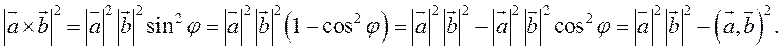
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле

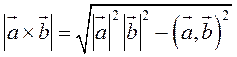.                                      (2.7)

ПРИМЕР.  Найти площадь параллелограмма, построенного на векторах  

.

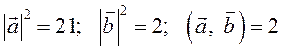По формуле (2.7):       

ЗАМЕЧАНИЕ 2. Направление вектора  можно также (кроме п.2) определить по правилу винта: направление вектора    совпадает с направлением поступательного  движения  винта  в  правой  резьбой  при  вращении  его в сторону  поворота первого вектора   ко второму  вектору   по кратчайшему пути (рис. 19).

Рис. 19

СВОЙСТВА  ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ

1.     

Доказательство: