Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 21

Поэтому выведем более  удобные  уравнения,  эквивалентные  (3.42),  то  есть  из  бесконечного  множества плоскостей, проходящих через данную прямую, выберем в некотором смысле  более заметную пару.

КАНОНИЧЕСКИЕ  УРАВНЕНИЯ  ПРЯМОЙ  В  ПРОСТРАНСТВЕ

Пусть в некоторой пдск задана прямая , проходящая через точку  параллельно ненулевому вектору . Такой вектор называется направляющим вектором этой прямой.

z A                M      О                             y x Рис. 49

Для произвольной точки    вектор где  – некоторый числовой множитель. Кроме того,  – радиус-вектор точки ,  – радиус-вектор точки  (рис. 49). Отсюда                           (3.43)

(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:

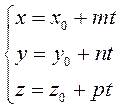                                                  (3.44)

(3.44) – параметрические уравнения прямой в пространстве,  – параметр.

Выразим из каждого уравнения (3.44) параметр:

.

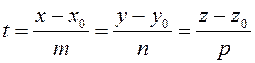Тогда 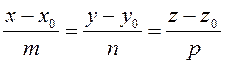                                                                    (3.45)

(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку   параллельно вектору .

Заметим, что уравнения (3.45) задают прямую  как результат пересечения плоскостей 

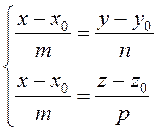, одна из которых параллельна , а вторая –   или как

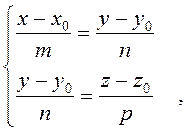
где первая плоскость параллельна , а вторая – .

Если прямая  проходит через две заданные точки  и , то  направляющий вектор этой прямой, поэтому из (3.45) получим:

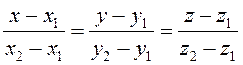                                           (3.46)

(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.

УГОЛ  МЕЖДУ  ПРЯМЫМИ  В  ПРОСТРАНСТВЕ

Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:

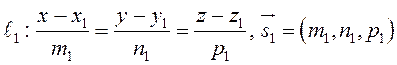
и 

.

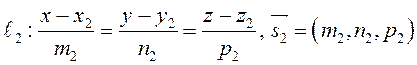ОПРЕДЕЛЕНИЕ. Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.

Из определения следует, что 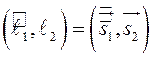. Если , то

.

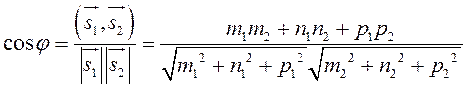1)  – условие перпендикулярности прямых.

2) 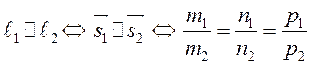 – условие параллельности прямых в пространстве.

ПРИМЕР. Найти угол между прямой 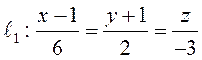 и прямой , проходящей через точки  и .

.

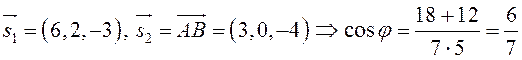Заметим, что уравнение прямой  имеет вид: 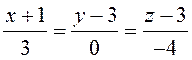 . В данном случае ноль в знаменателе  писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости . Эта прямая является результатом пересечения плоскосте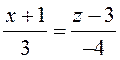й   и .

ПРИВЕДЕНИЕ  ОБЩИХ  УРАВНЕНИЙ  ПРЯМОЙ 

В  ПРОСТРАНСТВЕ  К КАНОНИЧЕСКОМУ  ВИДУ

Рассмотрим  прямую  , заданную  общими  уравнениями (3.42) в пространстве:

.

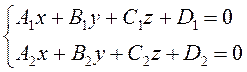Привести эти уравнения к каноническому виду можно двумя способами:

1) найти координаты какой-либо точки , лежащей на ,  ее направляющий вектор  и написать уравнения (3.45);

2) найти координаты двух точек, лежащих на , и воспользоваться уравнениями (3.46).

1 способ. Координаты точки  – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так как ранги основной и расширенной матриц , а число неизвестных .

 – направляющий вектор прямой , поэтому , где  – нормаль плоскости , а  – нормаль плоскости . Из определения векторного произведения векторов следует, что тогда  . Так как  – произвольный вектор, параллельный , то будем  считать, что  .

ПРИМЕР. Привести уравнения прямой 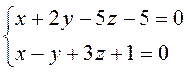  к каноническому виду.

Найдем какое-нибудь частное решение этой системы: пусть, например, 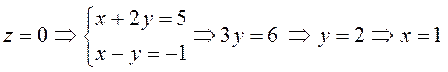, то есть точка  лежит на прямой.

.

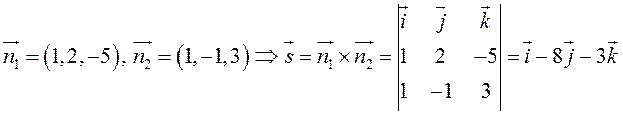Таким образом, 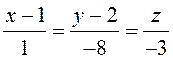  – канонические уравнения данной прямой.

2 способ. Найдем два произвольных частных решения системы уравнений, задающей прямую.

В рассмотренном примере  . Пусть теперь

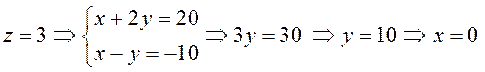, тогда  – направляющий вектор  прямой, который отличается от найденного ранее только знаком. Поэтому  уравнения 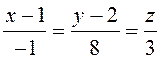   совпадают (с точностью до знака) с уже найденными.

УГОЛ  МЕЖДУ  ПРЯМОЙ  И  ПЛОСКОСТЬЮ

ОПРЕДЕЛЕНИЕ. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

Пусть в некоторой пдск заданы плоскость

и прямая 

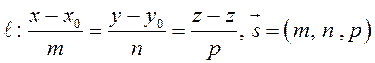                                  (рис. 50).