Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 12

Чтобы найти высоту, воспользуемся формулой 

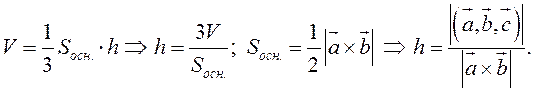
По формуле (2.7)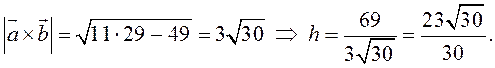 

Глава 3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

ПРЯМАЯ  НА  ПЛОСКОСТИ.

ОБЩЕЕ  УРАВНЕНИЕ  ПРЯМОЙ  НА  ПЛОСКОСТИ

Докажем, что всякая прямая на плоскости задается в любой пдск  уравнением первой степени относительно двух переменных.

Если  – некоторая точка на прямой , а  – вектор, перпендикулярный ей, то, во-первых, через  перпендикулярно   проходит единственная прямая на плоскости, а, во-вторых,  для любой точки  вектор . Таким свойством обладают только точки, лежащие на  .

y                                                   О                                           x Рис. 22

Чтобы вывести уравнение прямой, зададим на плоскости пдск . В этой системе координат   . Пусть  – произвольная точка на . Тогда (рис. 22 )   Так как , то по свойству 5 скалярного произведения  – векторное уравнение прямой  .

, поэтому по формуле (2.5) получим

.                                           (3.1)

Координаты точек, лежащих на прямой , связаны соотношением (3.1). Если же , то  не перпендикулярен  , значит, координаты  не будут удовлетворять полученному уравнению. Поэтому (3.1) – уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору. Заметим, что это уравнение линейно относительно переменных   и .

ОПРЕДЕЛЕНИЕ. Любой ненулевой вектор , перпендикулярный прямой , называется ее нормальным вектором, или нормалью.

(3.1)  . Обозначая , получим

                                             .                                                        (3.2)

(3.2) – общее уравнение прямой на плоскости,  – нормаль .

УРАВНЕНИЕ  ПРЯМОЙ  С НАПРАВЛЯЮЩИМ  ВЕКТОРОМ

ОПРЕДЕЛЕНИЕ. Любой ненулевой вектор , параллельный прямой, называется ее направляющим вектором.

Если  – некоторая точка на прямой , а  – вектор, параллельный ей, то, во-первых, через  параллельно   проходит единственная прямая, а, во-вторых,  для любой точки вектор . Таким свойством обладают только точки, лежащие на  .

Чтобы вывести уравнение прямой, зададим на плоскости пдск . В этой системе координат .

Пусть  – произвольная точка на . Тогда  и  Запишем условие коллинеарности векторов:

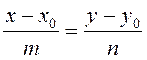.                                                     (3.3)  

(3.3) – уравнение прямой на плоскости с направляющим вектором.                  

Если , то  – направляющий вектор прямой  , поэтому уравнение прямой, проходящей через две точки имеет вид:

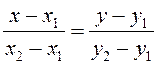                                                 .                                                    (3.4)

УРАВНЕНИЕ  ПРЯМОЙ  С  УГЛОВЫМ  КОЭФФИЦИЕНТОМ

Пусть   – направляющий вектор прямой , и  не параллельна оси , тогда .

ОПРЕДЕЛЕНИЕ. Угловым коэффициентом прямой  называется число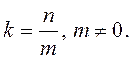

Очевидно, что если   – угол между прямой  и положительным направлением оси ОХ, то  .

Рассмотрим уравнение (3.3)  прямой с направляющим вектором :

  .

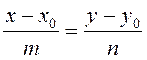
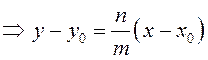Отсюда следует  (3.5) – уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку  :

                                                 (3.5)

Из (3.5) получим  . Обозначим , тогда

                                          .                                                          (3.6)

(3.6) – уравнение прямой с угловым коэффициентом.

УГОЛ  МЕЖДУ  ПРЯМЫМИ  НА  ПЛОСКОСТИ

ОПРЕДЕЛЕНИЕ. Углом между двумя прямыми на плоскости называется любой из двух смежных углов, образованных ими при пересечении. Если прямые параллельны, то угол между ними равен   или  радиан.

Пусть прямые заданы общими уравнениями.

y                                О                                 x Рис. 23

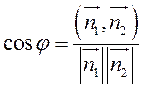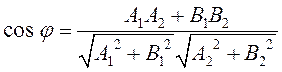                     или        .                   (3.7)

Условие параллельности прямых:

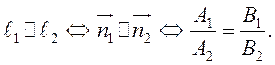
Условие перпендикулярности прямых: 

.

Рассмотрим случай, когда прямые заданы уравнениями с угловым коэффициентом.

y                         О                                             x Рис. 24

Так как   (рис. 24  ), то . Условие параллельности прямых:    . Условие перпендикулярности:     . Так как   не существует, то  .