Математика \ Математика

Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 23

ПОВЕРХНОСТИ  ВРАЩЕНИЯ

ОПРЕДЕЛЕНИЕ. Поверхностью вращения называется поверхность, полученная в результате вращения плоской кривой вокруг оси, лежащей в ее плоскости.

Из определения следует, что сечением такой поверхности любой плоскостью, перпендикулярной оси вращения, является окружность.

Пусть в плоскости  задана кривая .  – координаты точки в плоской системе координат . Эта кривая вращается вокруг оси . Выведем уравнение поверхности вращения.

z

 


О1          

M

О                              y

x

Рис. 57

Пусть  – произвольная точка на поверхности,  – центр окружности сечения, проходящего через точку , а  – точка, лежащая  на кривой и одновременно в  рассматриваемом сечении (рис. 57).

Тогда   – радиусы сечения.

Но                              .

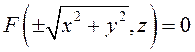Таким образом, уравнение поверхности вращения получим, если в уравнении кривой  заменим на , а  – на . Тогда получим:  – уравнение поверхности вращения ( – ось вращения).

Очевидно, что если кривая  вращается  вокруг , то уравнение поверхности вращения имеет вид:  .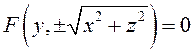  

Уравнение кривой

Ось вращения

Уравнение поверхности

 

НЕКОТОРЫЕ  ПОВЕРХНОСТИ  ВТОРОГО  ПОРЯДКА

1. Пусть эллипс 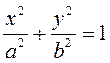 вращается вокруг оси .

z

 


a

О                 b             y

a

x

Рис. 58

Полученная поверхность является поверхностью второго порядка, так ее уравнение  – второй степени относительно переменных . Она называется эллипсоидом вращения (рис. 58).

Поверхность, задаваемая уравнением  , называется трехосным эллипсоидом.

2. Если гипербола 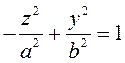  вращается вокруг оси , то уравнение

                                z

b      О     by

x

Рис. 59

поверхности вращения имеет вид 

или

.

Такая поверхность называется однополостным гиперболоидом вращения (рис. 59).

3. Если гипербола 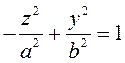 вращается вокруг оси , то уравнение поверхности имеет вид 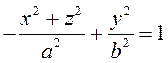  или 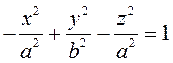. Такая поверхность называется двуполостным гиперболоидом вращения (рис. 60).

                                                        z

 


                                                 -b

О        by

x

Рис. 60

                                     z

 


О                               y

x

Рис. 61

4. Если пара пересекающихся прямых   вращается вокруг оси , то получается  конус вращения с уравнением      

или

             (рис. 61).

z

О                      y

x

Рис. 62

5. При вращении параболы  вокруг оси  получается поверхность , которая называется эллиптическим параболоидом вращения (рис. 62).

Библиографический список

1. Ефимов, Н.В. Квадратичные формы и матрицы / Н.В.Ефимов. – М.: Наука, 1972. – 160 с.

2. Киркинский, А.С. Линейная алгебра и аналитическая  геометрия. Учебное пособие / А.С.Киркинский. – М.: Академический Проект, 2006. – 256 с.

3. Шипачев, В.С. Основы высшей математики / В.С. Шипачев. – М.: Высш. шк., 1998. – 200 с.

4. Шнейдер В.Е. Краткий курс высшей математики / В.Е.Шнейдер, А.И. Слуцкий, А.С. Шумов. – М.: Высш. шк. 1978. – Т.2.

.    

 

 

 

Редактор

Компьютерная верстка

ИД 06039 от 12.10.01

Подписано в печать                    Формат 60х84  1/16

Бумага офсетная. Отпечатано на дуплекаторе.

Усл.печ.л.       Уч.-изд.л.

Тираж       экз.        Заказ

 


Издательство ОмГТУ. 644050, Омск, пр-т Мира, 11

Типография ОмГТУ

Скачать файл