Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 16

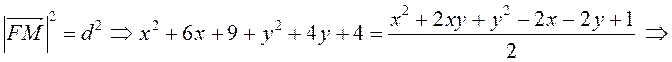
 – уравнение искомого геометрического места точек.

У               -3                                 x F -2       Рис. 36

Если оси координат системы   повернуть на угол  так, чтобы одна из них стала параллельна директрисе, а затем перенести  начало координат в точку  – вершину параболы, то в новой системе   уравнение  параболы будет каноническим    (рис. 36).

ЗАМЕЧАНИЕ. Можно показать, что, кроме окружности, эллипса, гиперболы, параболы и вырожденных случаев, указанных в замечаниях, других кривых второго порядка не существует.

ПРЕОБРАЗОВАНИЯ  КООРДИНАТ  НА  ПЛОСКОСТИ

1. Параллельный перенос координатных осей.

Пусть на плоскости задана пдск ХОУ. Будем называть ее “старой”. “Новая” система координат   получена из “старой” параллельным переносом осей в точку  .  Выясним, как связаны координаты   и   одной и той же точки М  в этих системах координат.

Так как  , то

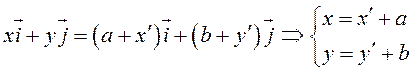
или 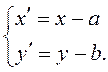                                                                                                      (3.23)

(3.23) – формулы параллельного переноса осей пдск.

Из рис. 38 очевидно, что

Так как  , то

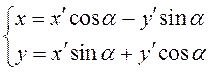                                                                                           (3.24)

(3.24) – формулы поворота координатных осей на угол , выражающие старые координаты точки через новые.

Если обозначить 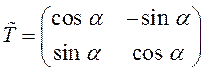 , , 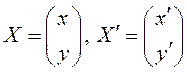то (3.24) можно переписать: . Так как то существует 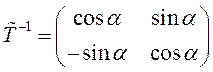 и

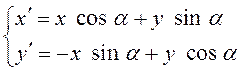                          (3.25)

(3.25) – формулы поворота координатных осей на угол , выражающие новые  координаты точки через старые.

ЛИНЕЙНЫЕ   ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ

Рассмотрим систему линейных уравнений:

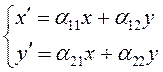                                                                                                   (3.26)

Каждой точке  плоскости  по формулам (3.26) можно поставить в соответствие  единственную точку  той же плоскости. При этом точка  называется образом точки , а точка  – прообразом точки .  Кроме того, уравнения (3.26) линейны относительно  и , поэтому будем говорить, что (3.26) определяют линейное преобразование плоскости в себя.

Преобразование (3.26) определяется матрицей 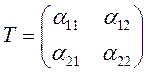 , которая называется матрицей линейного преобразования. Обозначая 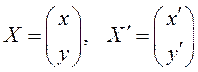,  (3.26) можно переписать в виде . Можно показать, что определитель   равен коэффициенту изменения площадей при линейном преобразовании (3.26). При этом  , если в результате преобразования направление обхода некоторого контура не меняется, и , если оно меняется на противоположное. Поясним это на примерах.