Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 13

ПРИМЕР. Даны вершины треугольника:. Написать:

а) уравнение медианы , б) высоты , в) найти угол между   и  (рис. 25).    

A          B              M      H      C Рис.25

а)  – середина ВС (см.  (2.4)). Напишем уравнение (3.4) прямой, проходящей через две точки: . Вектор  – направляющий вектор прямой  .

Перепишем уравнение  медианы в общем виде: 

 – нормаль АМ.

б)  – нормаль . Уравнение прямой (3.1), проходящей через точку  перпендикулярно вектору :

в) . По формуле (3.7)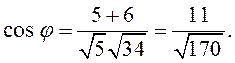  

РАССТОЯНИЕ  ОТ  ТОЧКИ  ДО  ПРЯМОЙ  НА  ПЛОСКОСТИ

Пусть  в некоторой пдск   задана прямая  и точка  Найдем расстояние от точки  до прямой

y M Р О                                   x Рис. 26

Пусть  – проекция точки  на  (рис. 26), тогда . Нормаль , где   – искомое расстояние, а  – скалярное произведение.

Следовательно,        .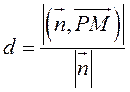

Так как  , то . Поэтому  

.

Отсюда 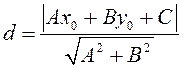                                      .                                             (3.8)

(3.8) – формула для вычисления расстояния от точки до прямой на плоскости.

ПРИМЕР.  Найти длину высоты

Уравнение  (3.4): 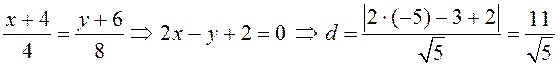  – искомая длина высоты АН.

КРИВЫЕ  ВТОРОГО  ПОРЯДКА.

ОКРУЖНОСТЬ

ОПРЕДЕЛЕНИЕ. Кривые второго порядка – плоские линии, которые в пдск   задаются уравнениями второй степени относительно двух переменных

ОПРЕДЕЛЕНИЕ. Окружностью называется совокупность точек  плоскости, равноудаленных от фиксированной точки, называемой ее центром.

Выведем уравнение окружности. Зададим пдск . Пусть  – фиксированная точка (центр окружности), а  – расстояние от точек окружности до ее центра (радиус окружности). Если  – произвольная точка окружности, то длина  равна .   

                                            (3.9)

Если точка   не лежит на окружности, то  и ее координаты уравнению (3.9) не удовлетворяют, поэтому, (3.9) – уравнение окружности с центром   радиуса .

Если  , то уравнение окружности примет вид:

                                                      .                                             (3.10)

(3.10) – каноническое уравнение окружности.

ПРИМЕР. Показать, что уравнение   задает окружность (то есть найти  ее центр и радиус).

Приведем  данное  уравнение  к  виду (3.9), выделив  полный квадрат по переменной  :

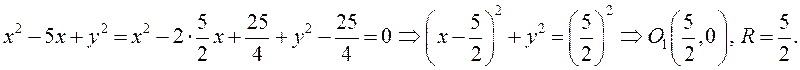
ПРИМЕР. Написать уравнение линии центров окружностей   и  .

Найдем центр второй окружности:       

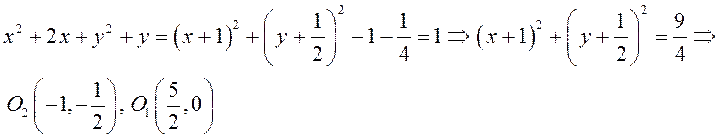
Уравнение прямой (3.4), проходящей через две точки:

.

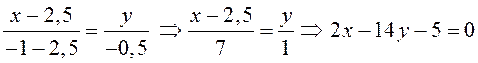Эллипс

ОПРЕДЕЛЕНИЕ. Эллипс – совокупность точек плоскости, сумма расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная и большая, чем расстояние между фокусами.

Чтобы вывести уравнение эллипса, выберем пдск следующим образом: ось абсцисс проведем через фокусы   и , а ось ординат – посередине отрезка  перпендикулярно оси абсцисс.  Обозначим расстояние между фокусами , тогда   . Пусть  – произвольная точка, лежащая на эллипсе, а   – сумма расстояний от точек на эллипсе до   и  ,   

У     О                  Х Рис. 27

по определению эллипса.  (рис. 27). Запишем в виде уравнения свойство точек, принадлежащих эллипсу, сформулированное в определении:    (3.11)

(3.11) – уравнение эллипса в выбранной системе координат. Преобразуем его к более простому (каноническому) виду. Для этого умножим (3.11)  на сопряженное выражение:

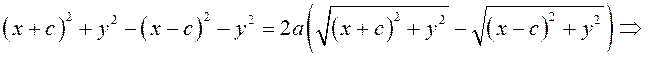
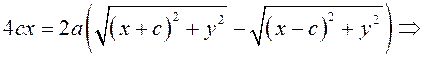
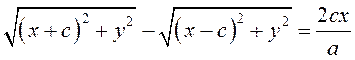                      .                        (3.12)

Сложим (3.11) и (3.12) и результат возведем в квадрат:

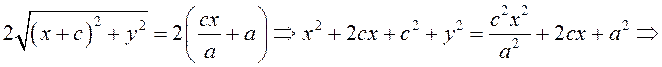
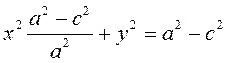                                                                      (3.13)

Так как по определению , то есть , то обозначим  . Тогда из (3.13) получим:

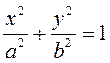                                                                                                             (3.14)

(3.14) – каноническое уравнение эллипса.