Глава 1. ЛИНЕЙНАЯ АЛГЕБРА
Этот раздел математики возник в связи с необходимостью решать системы линейных уравнений.
Рассмотрим систему линейных уравнений:
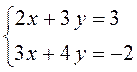 .
.
Чтобы решить ее, можно, например, выразить одну из
переменных из первого уравнения, подставить во второе, после чего найти
неизвестные ![]() и
и ![]() .
.
Однако можно найти решение быстрее: легко убедиться, что
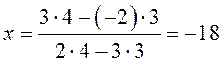
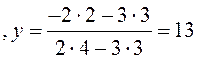 .
.
Способ получения этого результата станет ясным, если рассмотреть таблицы, составленные из коэффициентов системы:
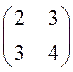
![]()
![]() ,
,
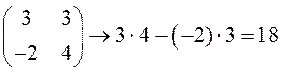 ,
,
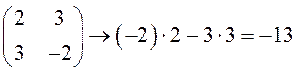
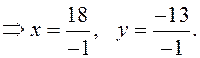
Такие таблицы называются матрицами второго порядка (так как в них две строки и два столбца), а соответствующие числа - определителями. Матрицы и определители играют важную роль при решении более сложных систем линейных уравнений, поэтому начнем изучение линейной алгебры с матриц.
МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
ОПРЕДЕЛЕНИЕ.
Числовой матрицей размера m![]() n
называется совокупность
n
называется совокупность ![]() чисел,
расположенных в виде таблицы, содержащей mстрок и n столбцов.
чисел,
расположенных в виде таблицы, содержащей mстрок и n столбцов.
![]() =
=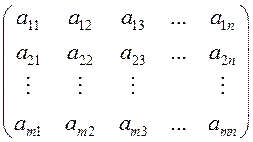 или
или ![]() =
= ![]() ,
, ![]() =1,2,…,
=1,2,…,![]() ,
, ![]() 1,2,…,
1,2,…,![]() .
.
![]() – элемент матрицы, стоящий на пересечении
– элемент матрицы, стоящий на пересечении ![]() -й строки и
-й строки и ![]() -го
столбца.
-го
столбца.
ОПРЕДЕЛЕНИЕ.
Если ![]() , то матрица называется квадратной
, то матрица называется квадратной ![]() -го порядка, в противном случае – прямоугольной.
-го порядка, в противном случае – прямоугольной.
Элементы
![]() ,
, ![]() = 1, 2,
…, n квадратной матрицы А образуют ее главную диагональ.
= 1, 2,
…, n квадратной матрицы А образуют ее главную диагональ.
Матрица размера ![]() называется матрицей-строкой, а матрица размера
называется матрицей-строкой, а матрица размера
![]() – матрицей-столбцом.
– матрицей-столбцом.
ПРИМЕР. 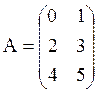 ,
, 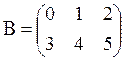 ,
, 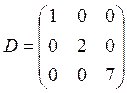 ,
, 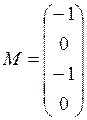
3х2 2х3 3х3 4х1
ОПРЕДЕЛЕНИЕ. Две матрицы называются равными, если они имеют одинаковый размер и равны их элементы, стоящие на одинаковых местах.
ПРИМЕР.
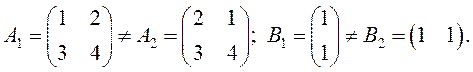
ОПРЕДЕЛЕНИЕ.
Квадратная матрица называется диагональной, если равны нулю все ее
элементы, расположенные вне главной диагонали, то есть ![]()
На
главной диагонали могут быть любые числа. Если все они равны 1, то диагональная
матрица называется единичной и обозначается буквой ![]() .
.
ПРИМЕР. 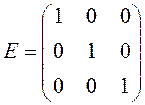 – единичная матрица третьего порядка.
– единичная матрица третьего порядка.
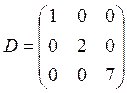 – диагональная матрица 3-го порядка.
– диагональная матрица 3-го порядка.
ОПРЕДЕЛЕНИЕ. Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.
ПРИМЕР.
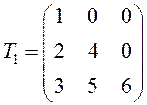 – треугольная матрица третьего порядка,
– треугольная матрица третьего порядка,
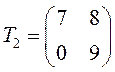 – треугольная матрица второго порядка.
– треугольная матрица второго порядка.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД МАТРИЦАМИ
К числу линейных относятся операции сложения и умножения на число.
ОПРЕДЕЛЕНИЕ.
Пусть ![]() =
=![]() и
и ![]() =
=![]() ,
, ![]() =1,2,…,
=1,2,…,![]() ,
, ![]() =1,2,…,
=1,2,…,![]() –
матрицы размера
–
матрицы размера ![]() . Матрица
. Матрица ![]() =
=![]() также размера
также размера ![]() называется
суммой матриц
называется
суммой матриц ![]() и
и ![]() , если
, если ![]() ,
, ![]() =1,2,…,
=1,2,…,![]() ,
, ![]() =1,2,…,
=1,2,…,![]() .
.
ПРИМЕР.
![]() =
=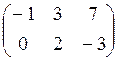 ,
, ![]() =
=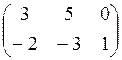
![]()
![]() =
=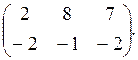
ОПРЕДЕЛЕНИЕ. Произведением матрицы ![]() =
=![]() размера
размера ![]() на число
на число ![]() называется
матрица
называется
матрица ![]() =
=![]() того же размера,
элементы которой
того же размера,
элементы которой ![]() ,
, ![]() =1,2,…,
=1,2,…,![]() , k=1,2,…,
, k=1,2,…,![]() .
.
ПРИМЕР. ![]() =
=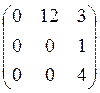
![]()
![]() =
=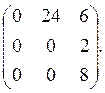
ОПРЕДЕЛЕНИЕ. Нулевой матрицей
![]() называется матрица, все элементы которой
равны нулю.
называется матрица, все элементы которой
равны нулю.
ОПРЕДЕЛЕНИЕ.
Матрица ![]() называется противоположной для
называется противоположной для ![]() и обозначается
и обозначается ![]() .
.
Очевидно, что ![]() для
любой матрицы А.
для
любой матрицы А.
ОПРЕДЕЛЕНИЕ.
Разностью матриц ![]() и
и ![]() одного размера называется сумма
одного размера называется сумма ![]() и обозначается
и обозначается ![]() .
.
ОПРЕДЕЛЕНИЕ. Результат конечного числа линейных операций над матрицами называется их линейной комбинацией.
ПРИМЕР.
Пусть ![]() =
=![]() ,
, ![]() =
=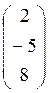 .
.
Матрица ![]() =
=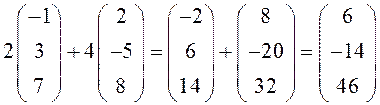 – линейная
– линейная
комбинация
матриц ![]() и
и ![]() с
коэффициентами 2 и 4.
с
коэффициентами 2 и 4.
СВОЙСТВА ЛИНЕЙНЫХ ОПЕРАЦИЙ
Если
![]() ,
, ![]() , и
, и ![]() – матрицы одного размера, а
– матрицы одного размера, а ![]() и
и ![]() –
числа, то, очевидно, справедливо следующее:
–
числа, то, очевидно, справедливо следующее:
1. ![]() –
свойство коммутативности сложения.
–
свойство коммутативности сложения.
2. ![]() – свойство ассоциативности.
– свойство ассоциативности.
3. ![]() – свойство дистрибутивности.
– свойство дистрибутивности.
4. ![]() .
.
5. ![]() .
.
ТРАНСПОНИРОВАНИЕ И УМНОЖЕНИЕ МАТРИЦ
Эти операции над матрицами не относятся к числу линейных.
ОПРЕДЕЛЕНИЕ.
Транспонированной матрицей ![]()
![]() для
матрицы
для
матрицы ![]() размера
размера ![]() называется
матрица размера
называется
матрица размера ![]() , полученная из
, полученная из ![]() заменой всех ее строк столбцами с теми же
порядковыми номерами.
заменой всех ее строк столбцами с теми же
порядковыми номерами.
То
есть, если ![]() =
=![]() , то
, то ![]()
![]() ,
, ![]() =1,2,…,
=1,2,…,![]() ,
, ![]() =1,2,…,
=1,2,…,![]() .
.
ПРИМЕР.
![]() =
=
![]()
![]()
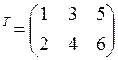 ;
; ![]() =
=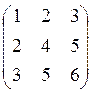 =
= ![]()
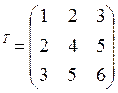
3х2 2х3 3х3 3х3
ОПРЕДЕЛЕНИЕ.
Если ![]() =
= ![]()
![]() , то матрица А называется симметрической.
, то матрица А называется симметрической.
Все диагональные матрицы симметрические, так как равны их элементы, симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.