Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 5

Рассмотрим систему  линейных уравнений с  неизвестными:

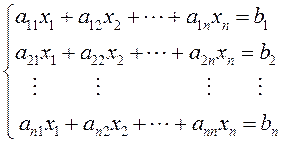                                          (1.10)

Матрица, составленная из коэффициентов системы (1.10)

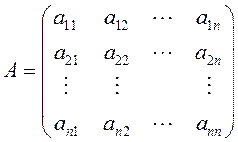, называется основной матрицей системы (1.10),  – основной определитель системы (1.10).

ОПРЕДЕЛЕНИЕ. Система линейных уравнений называется Крамеровской, если

1) число уравнений равно числу неизвестных;

2) основной определитель не равен нулю.

Рассмотрим матрицы 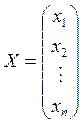    и 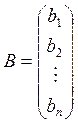  :    Х – столбец неизвестных,

В – столбец правых частей. Очевидно, что система (1.10) может быть записана в виде матричного уравнения

                                                                                                         (1.11)

ОПРЕДЕЛЕНИЕ. Совокупность  чисел  называется решением системы (1.10), если каждое из уравнений  системы обращается в верное числовое равенство при подстановке в него чисел  вместо соответствующих переменных 

ТЕОРЕМА. Всякая Крамеровская система имеет решение, причем одно.

ДОКАЗАТЕЛЬСТВО. По условию  Значит, для основной матрицы А системы существует обратная матрица . Умножим (1.11) на  слева:

 

                                                     (1.12)

По формуле (1.12) определяется каждое из неизвестных  то есть находится решение системы (1.10), причем оно единственно, так как единственна обратная матрица

ЗАМЕЧАНИЕ. Способ решения системы (1.10) по формуле (1.12) называется матричным способом решения системы линейных уравнений.

ПРИМЕР.  Решить систему уравнений матричным способом:

              

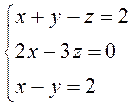
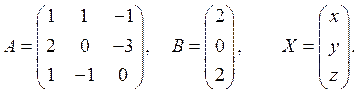
В предыдущем примере  было показано, что , значит, систему матричным способом решить можно. Там же была найдена обратная матрица

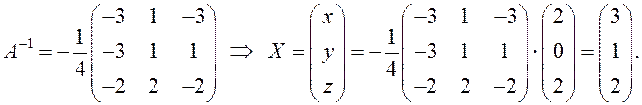
Таким образом,   Проверкой убеждаемся, что решение найдено верно.

ЗАМЕЧАНИЕ. Матричный способ удобен, когда надо решить несколько  Крамеровских  систем, которые отличаются только правыми частями.

Вернемся к равенству (1.12). Из него следует, что

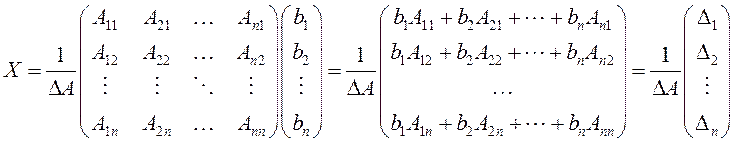, поэтому 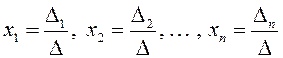                           ,                                    (1.13)                                                           где ,  – определитель матрицы, полученной из А заменой ее -го столбца на столбец правых частей системы (1.10) ,  = 1,2,…,. Формулы (1.13) называются формулами Крамера.

РАНГ МАТРИЦЫ.  ЭЛЕМЕНТАРНЫЕ  ПРЕОБРАЗОВАНИЯ

ОПРЕДЕЛЕНИЕ.  Минором  порядка   матрицы А называется определитель -го порядка, составленный из элементов матрицы А, стоящих  на пересечении произвольно выбранных  строк и столбцов без изменения порядка их следования.

ПРИМЕР. Рассмотрим матрицу .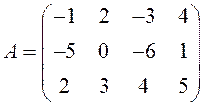

Миноры первого порядка – каждый элемент матрицы .

Миноры  второго порядка: 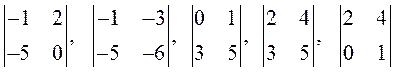  и так далее.

Матрица   имеет всего 18 миноров второго порядка.

Миноры третьего порядка: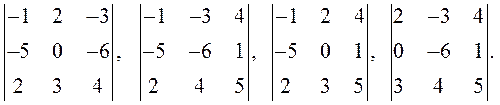      

Миноров четвертого порядка у этой матрицы нет.

ТЕОРЕМА. Если все миноры -го порядка матрица А равны нулю, то равны нулю и все миноры старших порядков, если они существуют.

ДОКАЗАТЕЛЬСТВО. Рассмотрим минор порядка . Это определитель -го порядка, который ( по свойству 7 ) можно разложить по элементам некоторой  строки (столбца ). В разложении будут алгебраические дополнения, которые с точностью до знака совпадают с минорами - го порядка и по условию равны нулю. Поэтому равен нулю и рассматриваемый минор порядка  Аналогично равны нулю и миноры старших порядков ,…, если они существуют, что и требовалось доказать.

ОПРЕДЕЛЕНИЕ. Рангом  матрицы А называется такое целое число , что среди ее миноров -го порядка есть хотя бы один ненулевой, а все миноры порядка () равны нулю.

Из доказанной теоремы следует, что, другими словами, ранг матрицы – это наивысший порядок отличного от нуля минора.

Будем обозначать  ранг матрицы .

Ранг матрицы равен нулю тогда и только тогда, когда ее миноры равны нулю, то есть если матрица нулевая.

ПРИМЕР.

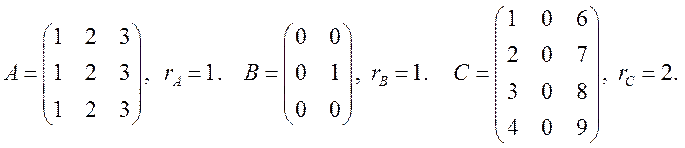
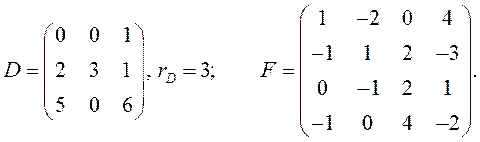
Матрица , очевидно, имеет ненулевой минор второго порядка, например, 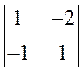, но все ее миноры третьего порядка – их всего 16 – равны нулю, поэтому  Для того чтобы обнаружить этот факт без трудоемких вычислений, введем понятие элементарных преобразований.

ОПРЕДЕЛЕНИЕ. Элементарными преобразованиями матрицы называются следующие действия: