Математика \ Математика

Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 17

y

                     

A

x

                      О                  B               

Рис. 41

ПРИМЕР. . 

, при этом направление обхода  от  к , затем к  – по часовой стрелке, а соответствующее направление обхода   – против часовой стрелки. Геометрически данное преобразование – растяжение вдоль   и  в 2 раза и отражение симметрично относительно оси  (рис. 41).

ОПРЕДЕЛЕНИЕ. Линейное преобразование (3.26) называется невырожденным, если  .

В этом случае существует обратная матрица   и можно найти . То есть, если , то не только у каждого прообраза существует единственный образ, но и наоборот: для каждого образа существует единственный прообраз. В этом случае говорят, что (3.26) устанавливает взаимно однозначное соответствие между точками плоскости, или линейное преобразование плоскости на себя.

Можно показать, что невырожденное линейное преобразование переводит прямую в прямую, а кривую второго порядка – в кривую второго порядка.

ПРИМЕР. Пусть 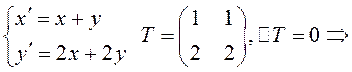 преобразование вырожденное.

Какими будут образы точек, лежащих, например, на прямой  (рис. 42)?

                            y                                   T                                       

                                           

1                                                                  2       

О        1                    x                                          1               

Рис. 42

Очевидно, что если , то , то есть у точки  существует бесконечное множество прообразов: все они лежат на прямой . Потому данное вырожденное линейное преобразование не устанавливает взаимно-однозначного соответствия между точками плоскости.

ПРИМЕР. Рассмотрим формулы (3.25):

.

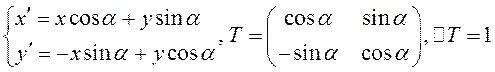Очевидно, что поворот осей пдск на угол   – линейное преобразование.

Так как это линейное преобразование невырожденное, то существует

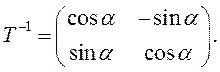
Заметим, что в этом случае  .

ОПРЕДЕЛЕНИЕ. Матрица  называется ортогональной, если . Линейное преобразование, матрица которого ортогональна, называется ортогональным.

Таким образом, поворот координатных осей – ортогональное линейное преобразование.

Можно показать, что если  – ортогональная матрица, то  (доказать самостоятельно). Таким образом, в результате ортогональных линейных преобразований на плоскости площади фигур остаются неизменными.

ПРОИЗВЕДЕНИЕ  ЛИНЕЙНЫХ  ПРЕОБРАЗОВАНИЙ

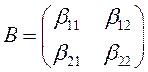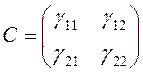Рассмотрим матрицы  и . Каждая из них определяет линейное преобразование плоскости. Если  – некоторая точка плоскости, то под действием линейного преобразования  с матрицей   она перейдет в точку :

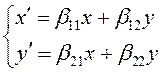                                                .                                               (3.27)

В свою очередь точка  под действием линейного преобразования  с матрицей   перейдет в точку :

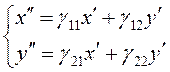                                               .                                               (3.28)  

Такое последовательное выполнение линейных преобразований называется их произведением: .

Покажем, что произведение линейных преобразований также линейное преобразование, и найдем его матрицу. Подставим (3.27) в (3.28):

.

То есть

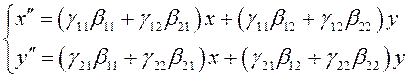                                                       (3.29)

(3.29)  – система линейных уравнений, а потому произведение линейных преобразований линейно. Матрица (3.29)  имеет вид:

.

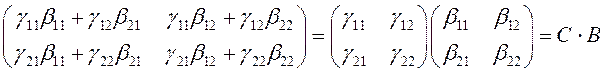Таким образом, матрица произведения линейных преобразований равна произведению их матриц. Само же правило умножения матриц, сформулированное в гл.1, находит объяснение в этом выводе.

ПРИВЕДЕНИЕ  КВАДРАТИЧНОЙ  ФОРМЫ

  К  КАНОНИЧЕСКОМУ  ВИДУ

ОПРЕДЕЛЕНИЕ. Квадратичной формой относительно двух переменных  и  называется однородный многочлен второй степени:

.                                 (3.30)

Уравнение  задает на плоскости кривую второго порядка, причем, так как вместе с точкой , лежащей на этой кривой, ей принадлежит и точка , кривая симметрична относительно начала координат, то есть является центральной кривой (эллиптического или гиперболического типа).

Скачать файл