Исследуем форму эллипса по его каноническому уравнению. Найдем точки пе-
|
У
-b Рис. 28 |
ресечения с осями координат:
Из (3.14) следует, что
Значит, эллипс расположен в
прямоугольнике со сторонами Кроме того, из уравнения
следует, что он симметричен относительно |
Ось, на которой лежат фокусы, называется фокальной
осью эллипса. Точки пересечения эллипса с осями симметрии называются его вершинами.
![]() – полуфокусное расстояние,
– полуфокусное расстояние, ![]() – малая полуось,
– малая полуось, ![]() – большая полуось эллипса и
– большая полуось эллипса и ![]() (рис. 28).
(рис. 28).
Отношение полуфокусного расстояния к длине большой
полуоси 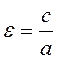 называется эсцентриситетом
эллипса. Он характеризует форму эллипса. Так как
называется эсцентриситетом
эллипса. Он характеризует форму эллипса. Так как ![]() , то
, то ![]() , и чем меньше
, и чем меньше ![]() , тем
больше эллипс похож на окружность. Для окружности
, тем
больше эллипс похож на окружность. Для окружности ![]()
ЗАМЕЧАНИЕ 1.
Уравнение эллипса, центр которого ![]() , а оси симметрии
параллельны координатным осям, имеет вид:
, а оси симметрии
параллельны координатным осям, имеет вид:
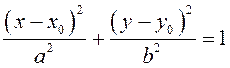 . (3.15)
. (3.15)
ЗАМЕЧАНИЕ 2.
К кривым второго порядка эллиптического типа относятся также мнимый эллипс 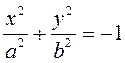 и точка
и точка 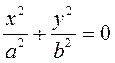 .
.
|
5
-4 О 4 Х
-5 Рис. 29 |
ПРИМЕР. Найти эксцентриситет эллипса Так как
|
Гипербола
ОПРЕДЕЛЕНИЕ. Гипербола – совокупность точек плоскости, модуль разности расстояний от которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
Чтобы вывести уравнение гиперболы, выберем пдск
следующим образом: ось абсцисс проведем через фокусы ![]() и
и
![]() , а ось ординат – посередине отрезка
, а ось ординат – посередине отрезка ![]() перпендикулярно оси абсцисс. Тогда
перпендикулярно оси абсцисс. Тогда ![]() – фокусы гиперболы (рис. 30). Пусть
– фокусы гиперболы (рис. 30). Пусть ![]() – произвольная точка, лежащая на гиперболе.
– произвольная точка, лежащая на гиперболе.
|
Х
Рис. 30 |
Запишем свойство точек, принадлежащих гиперболе, сформулированное в определении: |
![]() , (3.16)
, (3.16)
(3.16) – уравнение гиперболы в выбранной системе координат ( «+» – если разность расстояний положительна, и «–» – если отрицательна). Чтобы привести это уравнение к более простому виду, умножим (3.16) на сопряженное выражение и выполним такие же действия, как при упрощении уравнения эллипса, после чего получим:
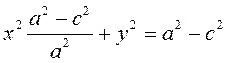 .
(3.17)
.
(3.17)
По
определению ![]() Обозначим
Обозначим ![]() , тогда
(3.17) перепишется в виде:
, тогда
(3.17) перепишется в виде:
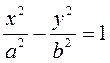 ,
(3.18)
,
(3.18)
(3.18) – каноническое уравнение гиперболы.
Исследуем форму гиперболы по ее каноническому уравнению.
Из (3.18) следует, что гипербола симметрична
относительно осей координат. Если 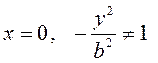 , значит, точек
пересечения с
, значит, точек
пересечения с ![]() нет; если
нет; если ![]() , то
, то ![]() . Точки
пересечения с осями симметрии называются вершинами гиперболы. Кроме
того, из (3.18) следует, что
. Точки
пересечения с осями симметрии называются вершинами гиперболы. Кроме
того, из (3.18) следует, что 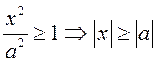 . Точка пересечения
осей симметрии называется центром гиперболы. Ось симметрии, на которой
расположены фокусы, называется фокальной осью. При этом фокальная ось
также называется действительной (с ней гипербола пересекается), а ось симметрии,
с которой гипербола не пересекается, называется ее мнимой осью.
. Точка пересечения
осей симметрии называется центром гиперболы. Ось симметрии, на которой
расположены фокусы, называется фокальной осью. При этом фокальная ось
также называется действительной (с ней гипербола пересекается), а ось симметрии,
с которой гипербола не пересекается, называется ее мнимой осью.
![]() – полуфокусное расстояние,
– полуфокусное расстояние, ![]() – действительная полуось,
– действительная полуось, ![]() – мнимая полуось. Отношение
полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом
гиперболы:
– мнимая полуось. Отношение
полуфокусного расстояния к длине действительной полуоси называется эксцентриситетом
гиперболы: 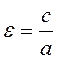 . Так как по определению
. Так как по определению ![]() , то
, то ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.